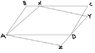
Proving Area Equality of Parallelograms ABCD & AXYZ

[galois427]

the prob ask me to prove that if parallelograms ABCD and AXYZ (see the attachment) are such that point X lies on side BC and point D lies on side YZ, the area of the 2 parallelograms are equal.

 

[TenaliRaman]

use vectors ...
AX = AB+BX
AZ = AD+DZ
take cross product of AX and AZ and simplify ...

-- AI

 

[galois427]

how would you express AX and AZ as a vector? I just set z=0 but when I took the cross product, i have a bunch of unknowns (x1,x2,x3,y0,y1).

 

[TenaliRaman]

we are working in the 2d plane so all vectors will be of form xi+yj tho we don't need to use this form here.
AX x AZ = (AB+BX) x (AD+DZ)
simplify this!
your goal is to show AX x AZ = AB x AD
tis a bit tricky but u can do it for sure!

-- AI

 

[galois427]

ok, this is what i got.

AX x AZ = (AB+BX) x (AD+DZ)
= (AB+BX) x AD + (AB+BX) x DZ
= AB x AD + BX x AD + AB x DZ + BX x DZ

AB x AD = (AX+XB) x (AZ+ZD)
= (AX+XB) x AZ + (AX+XB) x ZD
= AX x AZ + XB x AZ + AX x ZD + XB x ZD

and that's where i get stuck. how do you go about proving that those 4 vectors are equal to the other 4 vectors? are you suppose to put in arbitary numbers?

 

[robphy]

You may be able to turn this geometric observation into a proof.

Extend ZDY and BXC and mark their intersection as M.
Imagine sliding AB to AX and DC to DM.
Parallelogram AXMD has the same area as ABCD.
Now slide XM to XY and AD to AZ.
Parallelogram AXYZ has the same area as AXMD.

 

[TenaliRaman]

Ah indeed robphy!

galois,
to continue with the idea ...
what is BX x AD? (hint : definition of cross product)
what is AB x DZ + BX x DZ ??
(hint : again u can use the definition of cross product here ... )

-- AI