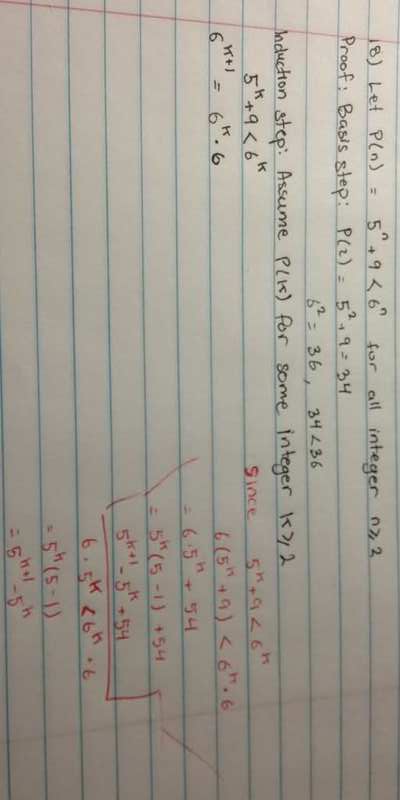Instinctlol
- 79
- 0
I am having trouble proving these. I cannot figure out how to get to the conclusion. Here is my attempt. The stuff in red is just side work and is not part of the proof. I always get stuck on these types of problems, can someone offer some tips on how to approach these kind of problems in general? Should I start with the right hand side or the left hand side of the inequality?