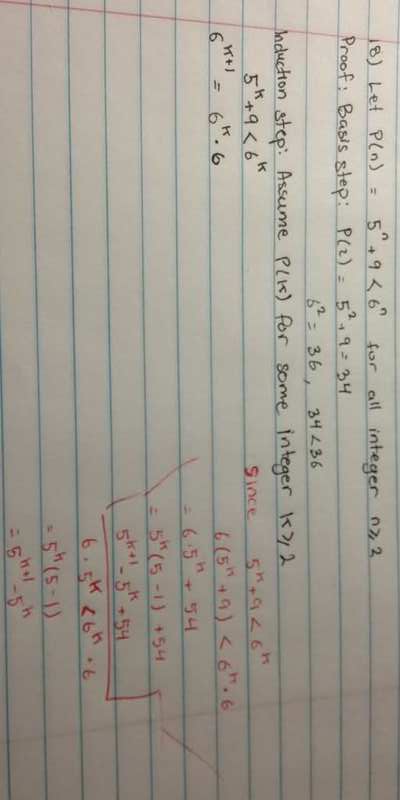SUMMARY
This discussion focuses on proving the inequality 5k+1+9 < 6k+1 using mathematical induction. The key approach involves leveraging the inductive hypothesis that 6k+1 = 6*6k > 6*(5k+9). The proof is structured by demonstrating that 5k+1 + 9 < 6(5k+9) simplifies correctly, confirming the validity of the inequality. The steps outlined provide a clear method for tackling similar problems in mathematical induction.
PREREQUISITES
- Understanding of mathematical induction principles
- Familiarity with inequalities and algebraic manipulation
- Knowledge of inductive hypothesis application
- Basic proficiency in algebraic expressions and simplification
NEXT STEPS
- Study the principles of mathematical induction in detail
- Practice proving inequalities using mathematical induction
- Explore examples of inductive proofs in textbooks or online resources
- Learn about common pitfalls in mathematical induction proofs
USEFUL FOR
Students, educators, and anyone interested in mastering mathematical induction techniques, particularly in proving inequalities.