Proving Inscribed Angle Theorem for Triangle Side Lengths
- Context: MHB
- Thread starter paulmdrdo1
- Start date
-
- Tags
- Triangle
Click For Summary
SUMMARY
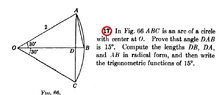
The discussion centers on proving the Inscribed Angle Theorem using triangle side lengths, specifically in triangle $OAB$, which is identified as isosceles. The key conclusion is that angle $BAC$ is half of angle $BOC$, leading to the determination that $BAC = 15^{\circ}$. The relationship between the central angle $BOC$ and the inscribed angle $BAC$ is established through the properties of isosceles triangles and circular segments.
PREREQUISITES- Understanding of the Inscribed Angle Theorem
- Knowledge of isosceles triangles and their properties
- Familiarity with central and inscribed angles in circles
- Basic geometry concepts related to angles and arcs
- Study the Inscribed Angle Theorem in detail
- Explore properties of isosceles triangles and their angle relationships
- Learn about central angles and their significance in circle geometry
- Practice problems involving angles in circles and their proofs
Students and educators in geometry, mathematicians focusing on circle theorems, and anyone interested in understanding the relationships between angles in circular segments.
Similar threads
High School
Understanding the Pythagorean Theorem
- · Replies 38 ·
- · Replies 59 ·
- · Replies 6 ·
- · Replies 13 ·
- · Replies 2 ·
- · Replies 1 ·
- · Replies 1 ·
- · Replies 1 ·
- · Replies 2 ·