Alfredoz
- 11
- 0
Dear All,
I need help on proving:
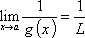
According to Pauls Online Notes,
we let ε > 0. Since [PLAIN]http://tutorial.math.lamar.edu/Classes/CalcI/LimitProofs_files/eq0075M.gif, there's a http://tutorial.math.lamar.edu/Classes/CalcI/LimitProofs_files/eq0076M.gif such that

I understand that l g(x) - L l < ε, but how do we derive l g(x) - L l < l L l / 2 ?
I need help on proving:
According to Pauls Online Notes,
we let ε > 0. Since [PLAIN]http://tutorial.math.lamar.edu/Classes/CalcI/LimitProofs_files/eq0075M.gif, there's a http://tutorial.math.lamar.edu/Classes/CalcI/LimitProofs_files/eq0076M.gif such that
I understand that l g(x) - L l < ε, but how do we derive l g(x) - L l < l L l / 2 ?
Last edited by a moderator: