Proving Triangle ABC's CD + AE = AC

[Michael_Light]

Homework Statement

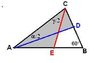
Given a triangle ABC with ∠ B = 60°. The bisectors of angle A and C intersect BC and AB at D and E respectively. Prove that CD + AE = AC.

Homework Equations

The Attempt at a Solution

I stuck on this question for hours already... what is the trick of proving this? Please help me.

 

[ehild]

First draw the triangle and the bisectors. Find relations among the angles. Find two triangles which contain the common side AC and either CD or AE as the other side. Apply the Law of Sines.

ehild

 

[Michael_Light]

Using angle bisector theorem, i get (EB/AC)= (AE)/(AC) and (BD)/(DC) = (AB)/AC). So by combining the results, i get

(AE + DC) / (AC) = [ (EB)/BC)] + [(BD)/(AB)]

(AE + DC) = (AC) [(EB)/BC)] + [(BD)/(AB)]

Am i in the correct path? How should i proceed?

 

[ehild]

Using angle bisector theorem, i get (EB/AC)= (AE)/(AC) and (BD)/(DC) = (AB)/AC).

The red should be BC.
To proceed, you need to use the given angle. Find out how the other angles in the triangle are related. Apply the Law of Sines to the triangles AEC and ADC.


ehild

 

[ehild]

I do it further as this is a nice problem.

In the blue triangle, η=60+γ/2,
In the yellow triangle, δ=60+α/2.

Applying the Law of Sines for both triangles,

AE/AC=sin(γ/2)/sin(60+γ/2),*

CD/AC=sin(α/2)/sin(60+α/2) **

α+60+γ=180°, so α=120-γ and α/2=60-γ/2.

(**) rewritten in terms of γ :

CD/AC=sin(60-γ/2)/sin(120-γ/2) ***

Applying the addition law of sine,

AE/AC=sin(γ/2)/(sin(60)cos(γ/2)+cos(6)sin(γ/2))

AE/AC=2sin(γ/2)/(√3cos(γ/2)+sin(γ/2))

CD/AC=(sin(60)cos(γ/2)-cos(60)sin(γ/2))/((sin(120cos(γ/2)-cos(120)sin(γ/2))

CD/AC=(√3cos(γ/2)-sin(γ/2))/(√3cos(γ/2)+sin(γ/2))

AE+CD=??