juef
- 27
- 0
Hi all,
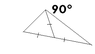
I'm having a hard time proving something. Let's say you have a triangle with a 90° angle. How can I prove that the length of the segment between the middle of the hypotenuse and the 90° angle is half the length of the hypotenuse itself?
Here's a little pic to help you...
Thanks a lot, and sorry for my pityful english! :)
john
I'm having a hard time proving something. Let's say you have a triangle with a 90° angle. How can I prove that the length of the segment between the middle of the hypotenuse and the 90° angle is half the length of the hypotenuse itself?
Here's a little pic to help you...
Thanks a lot, and sorry for my pityful english! :)
john