A Pullback of F on Manifolds: What Matrix Do We Take Determinant Of?

[Rico1990]

Hey,
we had in the lecures the following:
Let M and N be smooth manifolds, and dim(M)=dim(N)=n, while $$x^i$$ and $$ y^i$$ are coordinate functions around $$p\in M$$ respective $$F(p) \in N$$, then we get for the pullback of F

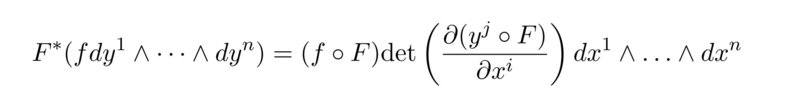
Which entries has the matrix we take the determinant of? I thaught of partial derivatives but am not sure.

 

[Orodruin]

Yes it is the partial derivatives of $y^j \circ F$ with respect to $x^i$, which is what the image you pasted says. This is just the Jacobian of the transformation $x^i \to y^j$ as subsets of $\mathbb R^n$.

 

[Rico1990]

Ok, thank you for your answer. But answer me please two last questions that arose. I deduce that these partial derivatives are defined, but they are vague in the sense, that $$x^i , y^i$$ are both functions the derivatives depend on. Is it the interest to leave them this vague or does one insert certain values so that the coordinate functions give „real" coordinates.
What is the use of this formula?

Best wishes Rico