Pulley system (ideal pulley) Find the angle with vertical line

[thirteenheath]

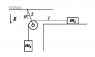
Ideal pulley and strings, no friction.The pulley and the second string don't move.
I need to find the numerical value of theta, the acceleration of the two blocks and the tensions.Accelerations and tension must be given in terms of m and g.I guess
2T1=T2
T1=m2*a
m1*g-T1=m1*aTo find theta I need to know the angle between T2 and T2*cosθ.
Are these equations correct?What is missing?

 

[ehild]

Hi thirteenheath, welcome to PF.

T2, the tension in chord 2 is not parallel with the forces of tension (T1, one horizontal and one vertical), chord 1 exerts on the pulley. Add them as vectors to get the force on the pulley. As the pulley does not move, the resultant of the tensions must be zero.
You can eliminate T1 from the last two equation and get the acceleration of the blocks.

ehild

 

[thirteenheath]

Thanks ehild!

Oh I see...So if I understood we'll have

T1=T2*cosθ

T1=T2*sinθ

Then cosθ=sinθ and θ=45°.

Plus, through the last two equations in the previous post we find that

a=m1*g/(m1+m2).

Now I just need to replace the acceleration in any of the previous equations to find the values of T1 and T2.

Is that it?

Thanks again. =)

 

[ehild]

Thanks ehild!

Oh I see...So if I understood we'll have

T1=T2*cosθ

T1=T2*sinθ

Then cosθ=sinθ and θ=45°.

Plus, through the last two equations in the previous post we find that

a=m1*g/(m1+m2).


Now I just need to replace the acceleration in any of the previous equations to find the values of T1 and T2.

Is that it?

Thanks again. =)

Yes, it will be all right.

ehild