playludesc
- 8
- 0
Hello all! I'm working with a particular pulley configuration and I realized after a few calculations that I don't have an accurate way to calculate one part of the set up.
Here's a quick MSPaint sketch showing what I need to solve for. If I know the outer diameter of both pulleys, and the RPM of the black pulley, how can I solve for the RPM at the outer diameter of the blue pulley? (If you care, this is regarding the jackshaft for my supercharger!)
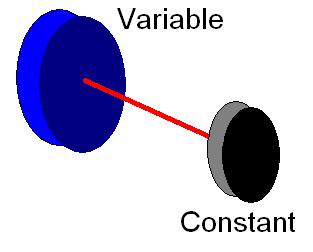
Thanks very much for your help!
Here's a quick MSPaint sketch showing what I need to solve for. If I know the outer diameter of both pulleys, and the RPM of the black pulley, how can I solve for the RPM at the outer diameter of the blue pulley? (If you care, this is regarding the jackshaft for my supercharger!)
Thanks very much for your help!