Pulling a crate across the floor with a rope at an angle

  • Thread starter jevans123
  • Start date
  • Tags
    Angle Rope
In summary: I see. You are asking for the normal force of the floor pushing up on the crate.Sorry, I misunderstood. I thought you were asking for the normal force of the floor pushing up on the crate. In that case, the expression would be:Ff=μkN
  • #1
jevans123
7
1
Homework Statement
I was told to be specific, so here it is:

Can you please help me answer this question that was given to me in the physics practice study guide? I am confused about this one and how to do so I would like someone to explain and walk me through how I should do this. Everybody keeps on telling me to reword this question and this is my second day just trying to ask a question on this platform. Can someone please help me out and I love you and I highly appreciate it if you did. Taking AP Physics 1 is quite challenging as a high schooler.

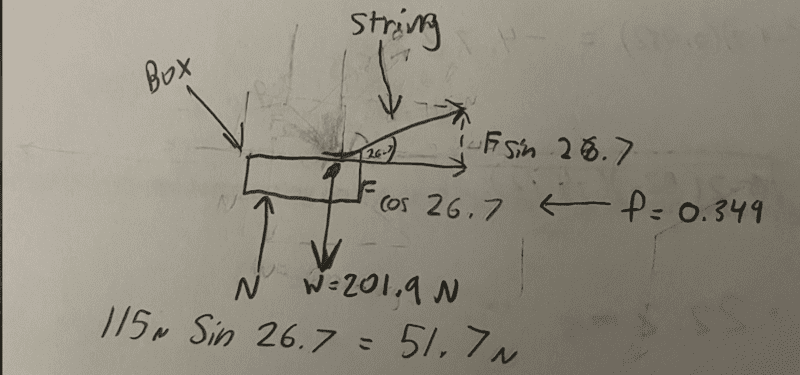
Roy pulls up at an angle on a rope attached to a crate to move the crate across a horizontal floor. The mass of the crate is 20.6 kilograms, Roy applies 115 newtons of force at an angle of 26.7 degrees, and the coefficient of kinetic friction between the crate and the floor is 0.349.

a. How hard does the floor push up on the crate?


b. What is the acceleration of the crate?
Relevant Equations
f = mu x N
I drew out a motion diagram and used 115N sin(26.7 degrees) = 51.7 N but It turns out to be wrong.

Screen Shot 2022-10-13 at 9.41.41 PM.png
 
Last edited:
Physics news on Phys.org
  • #2
jevans123 said:
Homework Statement:: Roy pulls up at an angle on a rope attached to a crate to move the crate across a horizontal floor. The mass of the crate is 20.6 kilograms, Roy applies 115 Newtons of force at an angle of 26.7 degrees, and the coefficient of kinetic friction between the crate and the floor is 0.349.

a. How hard does the floor push up on the crate?b. What is the acceleration of the crate?
Relevant Equations:: f = mu x N

I drew out a motion diagram and used 115N sin(26.7 degrees) = 51.7 N but It turns out to be wrong.
You will have to be more specific than that in your attempts. You are not giving any reasoning or even stating what you are trying to compute.
 
  • Like
  • Sad
Likes topsquark and jevans123
  • #3
I'm sorry, what does that even mean? Why are people just unwilling to help? Like I genuinely am asking a question and everybody just does some weird homework template and ohhh I haven't given enough detail and all. Like I am just asking for help and if you can't help then what is the point of commenting what you commented? I'm new so it would be nice to explain but I'm just so confused right now. What does "simultaneity" even mean and how is that even relevant?!
 
  • #4
jevans123 said:
What does "simultaneity" even mean and how is that even relevant?!
The word "simultaneity" appears in the signature that @Orodruin uses. It has nothing whatsoever to do with the response he provided.
jevans123 said:
a. How hard does the floor push up on the crate?
[...]
jevans123 said:
I drew out a motion diagram and used 115N sin(26.7 degrees) = 51.7 N but It turns out to be wrong.
Responding to the only work that was shown...

You have correctly calculated the vertical component of the tension force on the crate. Is that the quantity that was requested for part a?
 
  • Like
Likes topsquark
  • #5
jbriggs444 said:
The word "simultaneity" appears in the signature that @Orodruin uses. It has nothing whatsoever to do with the response he provided.

[...]

Responding to the only work that was shown...

You have correctly calculated the vertical component of the tension force on the crate. Is that the quantity that was requested for part a?
Well, the reason why I calculated the vertical component was because it was asking for how hard does the floor push up on the crate which is essentially the normal force and the term "up" tells me to find the vertical component. I don't think that is all to it but its all that I have gotten and understood.
 
  • #6
jevans123 said:
Well, the reason why I calculated the vertical component was because it was asking for how hard does the floor push up on the crate which is essentially the normal force and the term "up" tells me to find the vertical component. I don't think that is all to it but its all that I have gotten and understood.
You are asked for the force of the floor on the crate.
You found the force of the rope on the crate.
Are those the same thing?

Have you drawn a free body diagram?
Can you make a list of the forces that act on the crate?
 
  • Like
Likes topsquark
  • #7
List:

so we have,

the box being pulled at an angle of 26.7 degrees at 115 Newtons of force

then we have the weight of the crate going directly downward, Oh wait you made me think. Mass is not the same as weight. So now I'm thinking I use the mass of the box which is 20.6kg and multiply that by the Earth's constant acceleration of 9.80 and now the weight is 201.9 Newtons directly downward.

then we have the coefficient of kinetic friction directed the opposite of the way of the box at 0.349
 
  • #8
jbriggs444 said:
Have you drawn a free body diagram?
jevans123 said:
the box being pulled at an angle of 26.7 degrees at 115 Newtons of force
Please show us this (your FBD) before we go much farther. You can upload a PDF of JPEG copy of your diagram by using the "Attach files" link below the Edit window. Thank you.
 
  • Like
Likes topsquark
  • #9
Screen Shot 2022-10-13 at 9.16.38 PM.png
 
  • #10
You don't show all forces acting on the block. The surface is also exerting a normal force and a force of kinetic friction.
 
  • #11
Screen Shot 2022-10-13 at 9.41.41 PM.png
 
  • #12
It is customary to draw the forces acting on the body as arrows with their tail on the body. See example below. Also, the force of friction is not 0.349. That number is the coefficient of kinetic friction. What is the expression that allows you to find the force of friction if you know the coefficient of kinetic friction?

FBD.png
 
  • Like
Likes berkeman and topsquark
  • #13
OHHH ok so it would be this:

Ff=μkFN

But you need normal force to find that and I don't have normal force yet. Is normal force just the equal to the weight (in Newtons) of the object
 
  • #14
No. You need to add all the forces that have vertical components and set the sum equal to zero because the acceleration is zero in that direction.
 
  • Like
Likes topsquark
  • #15
jevans123 said:
OHHH ok so it would be this:

Ff=μkFN

But you need normal force to find that and I don't have normal force yet. Is normal force just the equal to the weight (in Newtons) of the object
You seem to be missing a major concept in this problem. Newton's 2nd Law says that net force acting on an object is equal to its mass times its acceleration. ie. ##F_{net} = ma##. Force and acceleration are vectors so this is a vector law. So we have the net force component in the horizontal direction and the net force component in the vertical direction.

We know from the problem statement that the acceleration component in the vertical (call it y) direction is 0 because we are not lifting the box. We also know (or need to calculate) an acceleration in the horizontal (call it x) direction. So we have
##\sum F_x =ma##

##\sum F_y = 0##

Break each of your forces into components and plug them into the Newton's 2nd Law equations.

-Dan
 
  • Informative
Likes jevans123

1. How does the angle of the rope affect the force needed to pull the crate?

The angle of the rope affects the force needed to pull the crate because it changes the direction of the force being applied. The greater the angle, the more the force is directed towards pulling the crate up rather than along the floor. This means that a greater force is needed to overcome the resistance of the crate against the floor.

2. Does the weight of the crate affect the amount of force needed to pull it?

Yes, the weight of the crate does affect the amount of force needed to pull it. The heavier the crate, the more force is needed to overcome the force of gravity and move it across the floor. This is why it is easier to pull a light crate compared to a heavy one.

3. Is it more efficient to pull the crate at a steeper or shallower angle?

It is more efficient to pull the crate at a shallower angle. This is because a steeper angle means that more force is directed towards pulling the crate up rather than along the floor. A shallower angle allows for more of the force to be directed towards moving the crate horizontally, making it easier to pull.

4. How does the type of surface affect the force needed to pull the crate?

The type of surface can greatly affect the force needed to pull the crate. A smooth and slippery surface, such as a polished floor, will require less force to pull the crate compared to a rough and uneven surface, such as a gravel road. This is because the rough surface creates more resistance against the crate, making it harder to move.

5. What other factors besides angle and weight can affect the force needed to pull the crate?

Other factors that can affect the force needed to pull the crate include the length and thickness of the rope, the strength and size of the person pulling, and the presence of any obstacles or friction on the surface. These factors can all impact the overall efficiency and ease of pulling the crate across the floor.

Similar threads

Direction of a rope with a ball inside an accelerating box
    • Introductory Physics Homework Help
Replies
5
Views
918
How Does Nick's Acceleration Change When His Friend Pulls the Rope?
    • Introductory Physics Homework Help
Replies
6
Views
2K
For a Pendulum: Knowing Acceleration Find Maximum Angle
    • Introductory Physics Homework Help
Replies
26
Views
2K
System of two pulleys and three masses
    • Introductory Physics Homework Help
Replies
22
Views
3K
David Morin's Rope around a Pole example
    • Introductory Physics Homework Help
Replies
8
Views
3K
Calculating Work on a Moving Crate with an Inclined Rope
    • Introductory Physics Homework Help
Replies
5
Views
6K
Solve for the tension in a rope pulling a box
    • Introductory Physics Homework Help
Replies
3
Views
2K
Physics G.11 Question on Forces/Newton's Laws and Friction
    • Introductory Physics Homework Help
Replies
5
Views
3K
Webpage title: Optimal Angle for Pulling a Crate with a Friction Rope
    • Introductory Physics Homework Help
Replies
8
Views
4K
Work done by friction force on an object?
    • Introductory Physics Homework Help
Replies
4
Views
5K

Hot Threads

Recent Insights

Back
Top