Nikitin said:
What does this notation mean?
##\vec x\mapsto \delta^{(3)}(\vec x-\vec y)## is the "function" that takes an arbitrary ##\vec x## to ##\delta^{(3)}(\vec x-\vec y)##.
Nikitin said:
Are you saying the position eigenfunction a dirac-delta function?
Not sure if it's appropriate to say "yes" to that, because I'm sure that someone would say that there's only one delta function on ##\mathbb R^3##, and it has its peak at ##\vec 0##. The "function" identified by the notation above has its peak at ##\vec y## (and there's one such "function" for each ##\vec y##). I'm inclined to call it a delta function, but I'm not sure everyone else would.
Nikitin said:
So you are saying an eigenfunction must always produce a sharp eigenvalue?
Not sure what you mean by "produce", but every eigenfunction has an eigenvalue. The specific case of the position operator is tricky though. It doesn't actually have an eigenfunction. The delta "function" isn't even a function. But it can be thought of as the wave"function" of a particle whose position has just been determined with perfect accuracy to be exactly at 0.
Nikitin said:
Well, even if the wave function ##\psi(x) = e^{i\vec p\cdot\vec x/\hbar}##, isn't it still an eigenfunction to the position operator ##x##? I mean, ##\hat{x} \psi(x) = x \cdot \psi(x)= x\psi(x)##
##\hat x\psi(x)=x\psi(x)## for all ##x\in\mathbb R## does
not imply that there's a number ##\lambda## such that ##\hat x\psi=\lambda\psi##. Define ##I:\mathbb R\to\mathbb R## by ##I(x)=x## for all ##x\in\mathbb R##. Let ##\psi## be an arbitrary function in the domain of ##\hat x##. Let ##x\in\mathbb R## be arbitrary. We have
$$(\hat x\psi)(x)=x\psi(x)=I(x)\psi(x)=(I\psi)(x).$$ Since x is arbitrary, this implies that ##\hat x\psi =I\psi##. But ##I## is a function, and it's not a constant function.
The following calculation is actually quite interesting. It sort of explains why the delta function is thought of as an eigenfunction of the position operator. Suppose that ##\hat x## has an eigenfunction. Denote it by f. Denote the eigenvalue by ##\lambda##. This means that ##\hat x f=\lambda f##. Let ##x\in\mathbb R## be arbitrary. We have
$$\lambda f(x)=(\lambda f)(x)=(\hat x f)(x)=xf(x).$$ This result tells us that if ##f(x)\neq 0##, then ##\lambda =x##. This is logically equivalent to if ##x\neq\lambda##, then ##f(x)=0##. So f takes every number to 0, except maybe ##\lambda##.
Nikitin said:
Indeed. And I think I will give up trying to understand why.
It's essentially just that an integral can be approximated by a sum. For each p, define ##u_p:\mathbb R\to\mathbb C## by ##u_p(x)=e^{ipx}## for all ##x\in\mathbb R##. (I'm using units such that ##\hbar=1##). A linear combination of several of the ##u_p## functions would look like this: ##\sum_k a_k u_{p_k}##.
$$\psi(x) =\frac{1}{\sqrt{2\pi}}\int \phi(p)e^{ipx}\mathrm dp =\frac{1}{\sqrt{2\pi}}\int\phi(p)u_{p}(x)\mathrm dp \approx \frac{1}{\sqrt{2\pi}}\sum_k \phi(p_k) u_{p_k}(x)\Delta p_k =\left(\sum_k \frac{\phi(p_k)\Delta p_k}{\sqrt{2\pi}}u_{p_k}\right)(x).$$
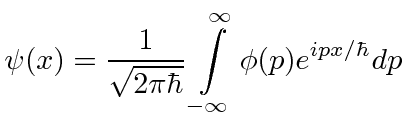 and
and
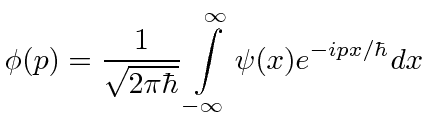 (and the rest of the text, for that matter) makes little sense to me. Is there any intuitive reason behind the formulas?
(and the rest of the text, for that matter) makes little sense to me. Is there any intuitive reason behind the formulas?