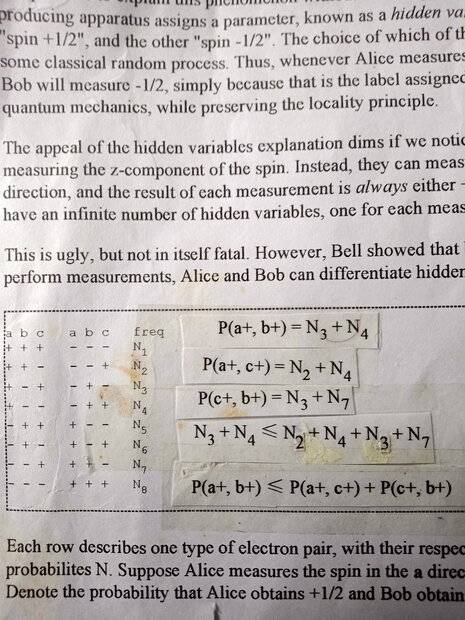morrobay
Gold Member
- 1,144
- 1,807
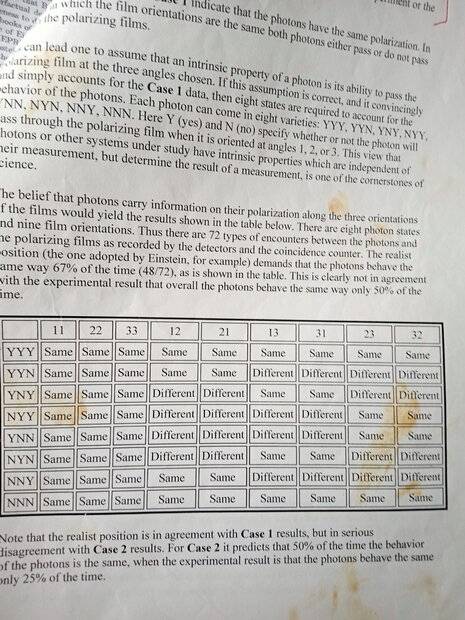
It seems the major premise for the derivation of Bell Inequalities is Counterfactual Definiteness for both electrons and photons : For electrons the spins at x, y, z directions are expected from conservation laws. See table. And for photons the eight polarization types along three orientations interact with nine pairs of detector settings. In each case electrons , photons the inequality does not hold. Seems this could be more from non Counterfactual Definiteness rather that quantum Non Locality. Especially since the expectations are based on three values and the experiments only measure two different settings. https://chem.libretexts.org/Bookshelves/Physical_and_Theoretical_Chemistry_Textbook_Maps/Quantum_Tutorials_(Rioux)/08:_Quantum_Teleportation/8.29:_Spooky_Action_at_a_Distance-_The_EPR_Experiment_with_Photons.