Quantum treatment of nonlinear susceptibility

[Konte]

Hi everybody,

In Robert W. Boyd's book "Nonlinear Optics", the quantum treatment of the nonlinear optical susceptibility lead to the next expression, for the second order case:

\chi^{(2)}_{ijk}(\omega_{\sigma},\omega_q,\omega_p)=\frac{N}{\hbar^2} P_F\sum_{mn} \frac{\mu_{gn}^i\mu_{nm}^j\mu_{mg}^k}{(\omega_{ng}-\omega_{\sigma})(\omega_{mg}-\omega_p)}

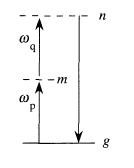
- At first time, I supposed \mu_{nm}=\langle{\phi_n} |\hat{\mu} |{\phi_m}\rangle where \phi_n and \phi_m are eigenstates of nonperturbated system. But when I saw the illustration (the same that I show you here), the levels n and m are virtuals !

My question is: in concrete case, how to define and calculate the matrix element \mu_{nm} ?

Thank you everybody.

* forgive me for my English.

 

[soarce]

$\mu_{nm}$ is the transition matrix element of the electric dipole operator: http://en.wikipedia.org/wiki/Transition_dipole_moment
The trick here is the sum over the all posible intermediate states (virtual states).

 

[Konte]

Thank you for your response soarce. But I always have a question:
When you say: "The trick here is the sum over the all posible intermediate states (virtual states)", are you meaning that the n and m levels are virtuals?

 

[soarce]

The $n$ and $m$ levels by themselves are eigenstates of the system. In your case the $n$ and $m$ are virtual in the sense that one has to sum over all posible states. In the case of the nonlinear susceptibility the system doesn't really pass through any $n$ or $m$ state, it more like a resonance phenomena: the three fields couple by the help of the atomic system.

Do you plan to compute the magnitude of the nonlinear susceptibility ?

 

[Konte]

Do you plan to compute the magnitude of the nonlinear susceptibility ?

Just now, I don't have computation to do, but I just want to understand this formula.

Let me have any physical system. After solving its nonpertubed Hamiltonian and finding eigenstates, I am thinking to myself : how can I finding the expression of \chi^{(2)} of the system? And I found this expression in Boyd's book.
So now, when you tell me to sum over all possible states, does the summation mean :

\sum_{mn}\mu_{mn}=\mu_{11}+\mu_{12}+\mu_{13}+...+\mu_{21}+\mu_{22}+\mu_{23}...

where 1,2,3,... refers to real eigenstates of system?

Is my understanding correct?

 

[soarce]

In the expression which you found the indexes $n$ and $m$ are linked also to $\mu_{gn}$ and $\mu_{mg}$. The sum would like something like this:

<br /> \sum_{nm}\mu_{gn}\mu_{nm}\mu_{mg} = \sum_{\underset{n \neq g}{n}} \mu_{gn} \left( \sum_\underset{m\neq n,g}{m} \mu_{nm}\mu_{mg}\right)<br />

Maybe you should study first a simpler example, e.g. two-photon transition, in order to understand how the sum over the virtual states is introduced. In your example the nonlinearity involves two virtual states (hence the double sum) with the initial and final state being the same.

 

[Konte]

Thank you much.

I will search from now something about two-photon transition that you advice me. But,could you, in parallel, advice me some internet link or books that explain well this question.

 

[soarce]

A direct search by Google gives you some lecture notes on two-ptohon transitions:
https://www.google.es/search?q=two-...-8&oe=utf-8&gws_rd=cr&ei=DED-VPHrDMz8UJ2KgcgL

Try to read the chapter "II.D Multiphoton processes" from Cohen-Tannoudji "Atom-Photon Interactions". It has a descriptive part where focuses on the physics of the phenomena and later address quantitatively the processes (see for instance chapter III "Nonperurbative calculation of transition amplitude"), although I find this last part a little bit hard to follow.

 

[Konte]

Thank you soarce. I get the Cohen Tannoudji's book from library now. I will read it and return here to tell you how about my understanding.