Question about fluids and Bernoulli's Equation

[remedemic]

High school student here trying to learn fluids. This is not a homework question, just a concept that I am trying to grasp but can't. The picture below is in my book:

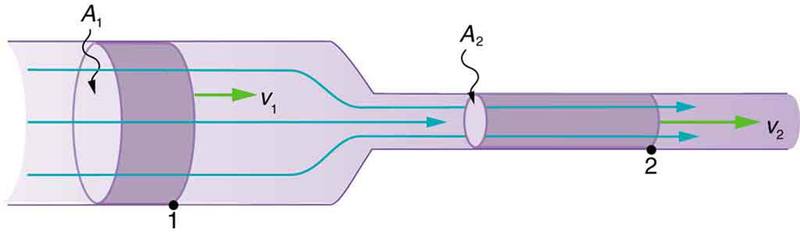
The book tells me that the acceleration of the fluid after experiencing the decrease in cross sectional area is due to a force that arises from the difference in pressures of the slower fluid and faster fluid. But the difference in pressures comes from the difference in velocities of the fluids. This leads me to conclude that the fluid accelerates because of a force that comes from the difference in pressure, which in turn comes from the difference in velocities. But the difference in velocities comes from the difference in pressure? This seems very cyclical to me. I asked an online tutor and he simply told me that it's a "chicken and egg" thing, but that didn't seem right to me.

Can someone help me understand this? Does the pressure difference come from the change in velocity or does the change in velocity from the pressure difference?

 

[tiny-tim]

hi remedemic!

Does the pressure difference come from the change in velocity or does the change in velocity from the pressure difference?

let's start again …

conservation of mass means that if the pipe gets narrower, then the velocity must increase (for an incompresisble fluid, such as most liquids)

this has nothing to do with pressure, it's just geometry and common-sense!

(the proportion of the velocities at two different points of the system will always be the same, no matter how you much about with the pressure at different points)

pressure is energy density (force per area = energy per volume)

conservation of energy means that if the velocity increases (ie the kinetic energy increases), then the pressure must decrease

(and bernoulli's equation is simply conservation of energy)

so the narrower pipe increases the velocity (conservation of mass), and decreases the pressure (conservation of energy)

 

[remedemic]

Thank you so much for the reply, I'm ready to rip my hair out after trying to learn this and I very much appreciate it. I just have a couple of questions about your explanation.

this has nothing to do with pressure, it's just geometry and common-sense!

Although geometry has to do with it, is there not some force acting on the fluid when it crosses over the lower cross-sectional area part? There has to be since the fluid is accelerating, right? Where does this force come from?

pressure is energy density (force per area = energy per volume)

I'm having trouble understanding exactly how pressure is measured at the two points in this pipe. What force is used and what area is used in measuring the pressure at the two points before and after the cross-sectional area decrease?

 

[tiny-tim]

hi remedemic!

Although geometry has to do with it, is there not some force acting on the fluid when it crosses over the lower cross-sectional area part? There has to be since the fluid is accelerating, right? Where does this force come from?

the force (that accelerates the fluid) comes from the sides of the tube

it's the same as the force you use when you squeeze a toothpaste tube …

you provide a sideways force, which makes all the molecules want to move faster sideways, and they hit other molecules, and the force gets spread out in all directions (that's what pressure is! ), resulting in a lengthwise force

I'm having trouble understanding exactly how pressure is measured at the two points in this pipe. What force is used and what area is used in measuring the pressure at the two points before and after the cross-sectional area decrease?

what force is used?

that's like asking what volume is used when we measure density …

we measure a small force F across an small area A, and divide

the area can be a cross-section, or it can be longitudinal, the result will be the same

(sometimes pressure is measured by a tube sticking upward out of the pipe … the height h of fluid in the tube, shows that the pressure is ρgh)

 

[remedemic]

you provide a sideways force, which makes all the molecules want to move faster sideways, and they hit other molecules, and the force gets spread out in all directions (that's what pressure is! ), resulting in a lengthwise force

When you say the "sideways" force, are you referring to the sides of the tube right after the decrease in cross sectional area that are "pushing down" on the fluid?

what force is used?

that's like asking what volume is used when we measure density …

we measure a small force F across an small area A, and divide

I meant WHICH force is used to calculate the pressure (F/A). Is it the force that the fluid behind a certain point is exerting on that point, or is it the force that the fluid is exerting on the walls of the tube? This is where my problem lies. I don't understand how pressure before the area decrease and after the area decrease is measured.

Thanks again for bearing with me. I really want a solid grasp on this concept.

 

[tiny-tim]

hi remedemic!

When you say the "sideways" force, are you referring to the sides of the tube right after the decrease in cross sectional area that are "pushing down" on the fluid?

i mean everywhere

consider a small cross-sectional slice of the pipe …

on the straight parts, the pressure on either side of the slice will be the same, so the net force is the same, and the speed is the same

on the narrowing part, the pressure on the front side is lower, so the net force is forwards, causing (or being caused by) acceleration

I meant WHICH force is used to calculate the pressure (F/A). Is it the force that the fluid behind a certain point is exerting on that point, or is it the force that the fluid is exerting on the walls of the tube?… I don't understand how pressure before the area decrease and after the area decrease is measured.

in these problems, there's no viscosity, and the pressure is the same over the whole of a cross-section, so the pressure on the walls is the same as the pressure in the middle

technically, it's the force at the point in question which is measured (to find the pressure at that point)

 

[rcgldr]

The source of the pressures for the incoming and outgoing fluid is not defined; they are coming from undefined external sources. Bernoulli assumes no external forces, so it only applies to the fluid once it's already flowing within the pipe. The mass flow within the pipe is constant at all points, otherwise mass would be accumulating within the pipe. If mass flow is constant and the fluid is incompressable, then the flow speed is proportional to the inverse of the cross sectional area. Since the flow speed is faster in the narrower section of the pipe, and there are no external forces, then some internal force causes the flow to accelerate, and this internal force is a pressure gradient where static pressure decreases relative to the speed^2 of the flow. Since there are no external forces involved for the fluid flowing within the pipe, the total energy of any volume of that fluid within the pipe is a constant and follows Bernoulli's equation.

 

[Jano L.]

Can someone help me understand this? Does the pressure difference come from the change in velocity or does the change in velocity from the pressure difference?

What you have is an instance of the infamous problem of what is cause and what is effect in a situation when both events happen at the same time.

The answer depends on whether you want to get common sense $causal$ description used in daily life, or understand what theoretical physics says.

In daily life, we describe things with causal talk. The part which we control directly gets labeled "cause", the part that is connected to this cause and mirrors its behaviour with some time lag gets labeled "effect".

For example, when the motor dies, first we begin pushing the car, and only later we see that it has some sensible velocity (it takes some time after the pushing began). Hence everybody thinks of force as the cause and the movement as the effect.

From this standpoint, in your question the water will acquire higher velocity only after some force is acting on it for some time, so the answer would be, the difference in pressures causes the water to change its velocity.

HOWEVER, in theoretical physics, we work with exactly formulated laws, that is with equations. Then the best answer I know to this and to other similar questions seeking cause is "in physics there is no absolute way to distinguish cause and effect". Whenever the force is applied, the first law of motion is

$$
\mathbf F= \frac{d\mathbf p}{dt},
$$

so if $\mathbf p =m\mathbf v$ as usual the acceleration is present at the same time the force is. There is no lag, so the acceleration cannot be called "effect". We just do not see the acceleration normally, we only see high enough velocity, so we tend to think there is a lag (J. Frenkel).

From this standpoint, if the flow is steady and laminar, the Bernoulli equation can be derived from the basic laws of fluid mechanics:


$$
p + \frac{1}{2}\rho v^2 + \rho gh = const.,
$$

which enables us to find what is the change in $p$, given the change in $v$, or what is the change in $v$, given change the in $p$. The basic laws give us no way for introducing such asymmetric roles for the two as the usage of "cause" and "effect" requires in daily talk.

 

[Andy Resnick]

<snip>
Can someone help me understand this? Does the pressure difference come from the change in velocity or does the change in velocity from the pressure difference?

Just to add to the good responses already posted, it's important to realize that what happens in the 'transition region' (where the tube narrows) is completely ignored in this simple analysis. The basic analysis looks only at two regions, each far removed from the transition region ("fully developed pipe flow").

When the flow is analyzed in more detail, a variety of "head losses" can occur depending on the detailed pipe geometry.

 

[Chestermiller]

The pressure difference between upstream and downstream is causing the fluid to accelerate. This is basically a case of F = ma. Upstream, the pressure is forcing each parcel of fluid to accelerate in the direction of flow. Downstream, the pressure is acting in the opposite direction. In the converging section, the pressure exerted by the converging wall is also pushing the fluid forward. The net effect is that the kinetic energy of a parcel of fluid exiting at location 2 is greater than the kinetic energy of a parcel entering at location 1. The upstream pressure at 1 comes from some pump or other device not shown in the figure. The downstream pressure could be the back pressure exerted by the atmosphere, if the pipe exits into the air.

 

[boneh3ad]

the force (that accelerates the fluid) comes from the sides of the tube

it's the same as the force you use when you squeeze a toothpaste tube …

you provide a sideways force, which makes all the molecules want to move faster sideways, and they hit other molecules, and the force gets spread out in all directions (that's what pressure is! ), resulting in a lengthwise force

In the converging section, the pressure exerted by the converging wall is also pushing the fluid forward. The net effect is that the kinetic energy of a parcel of fluid exiting at location 2 is greater than the kinetic energy of a parcel entering at location 1.

This is not really accurate. When you squeeze a tube of toothpaste, the toothpaste moves as a result of the resultant force in the axial direction of your radial squeeze (pretending this is cylindrical, or course). If you squeeze in the middle, some toothpaste goes to the back of the tube and some goes forward because there is some force going in both directions when you squeeze in.

In the pipe situation above, the force on the fluid from the constriction would both oppose the flow and be directed inward radially. The component in opposition to the flow is mathematically very similar to a drag-type force (i.e. it's dissipative) and is in part what leads to the head loss associated with the pipe constriction mentioned briefly by Andy Resnick.

The inward component of that force would tend to accelerate nearby individual molecules on the microscopic scale inward radially, but the net effect of that force on the continuum is going to be nothing since it is exactly balanced by the identical force coming from the other side of the constricted pipe. Whatever axial force is generated by the desired inward motion of the wall force is simply the molecular nature of the axial force previously described, and will oppose the flow.

This force is completely ignored by the Bernoulli analysis posited by the OP, and is typically accounted for by the use of a head loss term, again as alluded to by Andy Resnick.

After the constriction, the fluid has more kinetic energy despite the effects of the forces of the constriction, not because of them.

For evidence about the direction of the force of the constriction, consider if you modeled the angled section (for simplicity, let's say the upper portion in the OP's figure) as a flat plate at angle of attack to the incoming free stream. Now, imagine you shot a stream of water at that plate and it was unattached to any other object, allowing it to move freely. Which direction would it travel? It would move up and to the right because that is the direction of the force on the plate from the stream. The equal and opposite force is that of the plate onto the water, and this is analogous to what occurs in the case of the wall of the pipe constriction.

in these problems, there's no viscosity, and the pressure is the same over the whole of a cross-section, so the pressure on the walls is the same as the pressure in the middle

Just a quick note, this would essentially be true in any such situation, even with viscosity. One of the fundamental concepts in boundary layer theory is that throughout the vertical height of a boundary layer, the static pressure is very nearly constant.

Bernoulli assumes no external forces, so it only applies to the fluid once it's already flowing within the pipe.

Bernoulli's equation does not assume that there are no external forces, and, in fact, often contains a body force term in its formulation. Any external forces must be conservative forces (e.g. gravity, electromagnetism), but Bernoulli's equation could certainly handle them. The real reason it only applies to the fluid once it is already flowing is because Bernoulli's equation assumes that the flow is steady. The equation applies to stationary fluid just fine, but that flow is uninteresting and accelerating that flow to some more interesting case violates the steady-state assumption.

I meant WHICH force is used to calculate the pressure (F/A). Is it the force that the fluid behind a certain point is exerting on that point, or is it the force that the fluid is exerting on the walls of the tube? This is where my problem lies. I don't understand how pressure before the area decrease and after the area decrease is measured.

Thanks again for bearing with me. I really want a solid grasp on this concept.

This can be done in practice a number of ways. Typically, it is a measure of the force that the fluid would exert on the walls of the pipe, otherwise known as the static pressure. This is usually measured using a static pressure port that consists of a small opening in the wall that takes on a small volume of fluid which itself is essentially stationary and takes on the static pressure of the flow. This tube is typically hooked up to either a manometer, which measures the pressure based on the height of a known height of some liquid (often water or mercury) or else it is hooked up to a pressure transducer, which measures the forces on a membrane of a known size as a result of the the fluid pressure.

To answer the rest of your question, I think the best place to start is Jano L.'s response. There is not necessarily a cause and effect here, but merely two sides of the same coin. The flow must go faster because you cannot accumulate mass or create voids of mass in a continuum (a fact modeled using a continuity equation), so when the pipe constricts, you have to fit that same mass flow through a smaller tube, so it must accelerate. Of course, a faster-moving fluid means more kinetic energy, and by using Bernoulli's equation, which is an energy conservation equation, you can show that as you speed up and increase kinetic energy, the potential energy must fall, and this is manifested as a drop in static pressure.

Of course, for something to accelerate, there must be a force. Consider, then, that the definition of static pressure is the stress (or force divided by area) exerted by one fluid element on an adjacent element. As you reach the end of the large pipe just before the constriction, you have a high pressure that matches the pressure in the rest of the pipe up to that point. As you decrease the area of the pipe, the flow speeds up and the static pressure falls, so while a fluid element just before the constriction is pushing in all directions against its neighbors with some pressure $p_1$, the next element to the right in a smaller cross-section is pushing all around it with another pressure $p_2 < p_1$. In essence, then, the element at $p_1$ is pushing just a little bit harder than the element at $p_2$, resulting in a net force to the right. This force is the accelerating force in the example.

In essence, then, there isn't really a need for a cause and effect relationship here. The flow must accelerate to conserve mass, which implies an increase in kinetic energy, which implies a decrease in pressure, which implies a force in the direction of the pressure decrease, which cyclically implies that the flow has accelerated. For a steady flow, this is all simultaneous.

 

[Chestermiller]

This is not really accurate. When you squeeze a tube of toothpaste, the toothpaste moves as a result of the resultant force in the axial direction of your radial squeeze (pretending this is cylindrical, or course). If you squeeze in the middle, some toothpaste goes to the back of the tube and some goes forward because there is some force going in both directions when you squeeze in.

Dear boneh3ad,
In my response, I wasn't referring to a tube of toothpaste. What I was saying was that, the pressure acts normal to each wall surface. In the converging section, the normal force exerted by the fluid pressure on the wall has a component in the axial direction. The wall exerts an equal an opposite force on the fluid. This is partially causing the fluid to accelerate axially. Additional axial forces are imposed on the fluid by pressure at the inlet and the outlet.

Please don't imply that I would invoke an analogy to a tube of toothpaste.

Chet

 

[rcgldr]

Bernoulli assumes no external forces, so it only applies to the fluid once it's already flowing within the pipe.

Bernoulli's equation does not assume that there are no external forces, and, in fact, often contains a body force term in its formulation. Any external forces must be conservative forces (e.g. gravity, electromagnetism), but Bernoulli's equation could certainly handle them.

Since the flow in the OP is essentially horizontal, I was ignoring the gravity term of Bernoulli's equation. The point I was getting at is some external forces are required to maintain the pressures at both ends of the pipe in the OP. Some external force is causing the fluid to flow into the larger section of pipe at the entry pressure, and another external force is resisting the flow exiting the smaller section of pipe, maintaining it's exit pressure.

 

[boneh3ad]

Dear boneh3ad,
In my response, I wasn't referring to a tube of toothpaste. What I was saying was that, the pressure acts normal to each wall surface. In the converging section, the normal force exerted by the fluid pressure on the wall has a component in the axial direction. The wall exerts an equal an opposite force on the fluid. This is partially causing the fluid to accelerate axially. Additional axial forces are imposed on the fluid by pressure at the inlet and the outlet.

Please don't imply that I would invoke an analogy to a tube of toothpaste.

Chet

I wasn't claiming you made a tube of toothpaste analogy; tiny-tim made that connection. Instead, the point he was trying to make with that analogy was related to the statement of yours that I was also addressing. I realize the force has an axial component, but that component acts counter to the flow, not with it. Whether you meant it or not, your first post according to my reading of it seemed to imply that the force of the wall onto the fluid was contributing or the sole factor in increasing the velocity of the flow through the contraction, which is not the case since the resultant force is against the flow, and that this is in part what causes the head loss inherent in a contraction. If that is not what you were implying, then I apologize.

Since the flow in the OP is essentially horizontal, I was ignoring the gravity term of Bernoulli's equation. The point I was getting at is some external forces are required to maintain the pressures at both ends of the pipe in the OP. Some external force is causing the fluid to flow into the larger section of pipe at the entry pressure, and another external force is resisting the flow exiting the smaller section of pipe, maintaining it's exit pressure.

Right, I understand the decision to ignore the gravity term. My point was about the fact that Bernoulli's equation makes no assumptions about the existence or non-existence of fluids under the action of external forces other than those forces must be conservative in nature. The OP, being new to the subject, may easy get confused based on how you originally worded it.

 

[rcgldr]

My point was about the fact that Bernoulli's equation makes no assumptions about the existence or non-existence of fluids under the action of external forces other than those forces must be conservative in nature. The OP, being new to the subject, may easy get confused based on how you originally worded it.

I'm not sure how to word this. For a given flow and initial pressure, Bernoulli explains the change in pressure of the fluid as it flows through the narrowing pipe, but it doesn't explain how the fluid got it's initial flow and pressure (the source of the fluid's initial energy).

 

[tiny-tim]

my toothpaste tube analogy was only to illustrate how a purely sideways external force can create a forwards internal force

i'm a small cube of fluid in the narrowing part of the OP's tube

i notice I'm being accelerated forwards

i wonder why … i realize I'm being pushed harder by molecules knocking into me from behind than from in front

i look to see why the molecules behind are pushing me at all, and i see that molecules behind them are pushing them, ultimately all the way back to the start of the pipe, where some interfering idiot with a piston (say) is providing an external forwards force

but that doesn't explain why the force in front of me is less than the force behind

so i look sideways, and i see that the molecules closer to the pipe are pushing the molecules closer to the centre, all the way back to the pipe itself, where the pipe itself (it's not its fault, it can't help it!) is providing the only other external force, a sideways (and partly backwards) one

and i see that ultimately, it's the magnitude of that sideways external force which is providing the extra energy (pressure = energy density), and it's providing more extra energy behind me than in front of me because the pipe is providing more sideways external force where it's wider​

(why the pipe is doing that, i can't see … i have to phone my friend bernoulli, and he tells me it's because of some complicated equation about conservation of energy)

EDIT: it doesn't have to be a fluid, it could eg be loosely packed ping-pong balls

 

[Jano L.]

...and i see that ultimately, it's the magnitude of that sideways external force which is providing the extra energy (pressure = energy density),...

Although your conclusion is correct, your explanation does not seem to be, or I do not understand it. Force due to the wall of the pipe (in the friction-less case) cannot provide energy to the fluid if the wall does not move. The only effect of the force of the wall in such case is to curve the trajectories of the fluid particles. Their acceleration is due to the forces of the other fluid particles, since there is a gradient of pressure in the fluid.

 

[Chestermiller]

I wasn't claiming you made a tube of toothpaste analogy; tiny-tim made that connection. Instead, the point he was trying to make with that analogy was related to the statement of yours that I was also addressing. I realize the force has an axial component, but that component acts counter to the flow, not with it. Whether you meant it or not, your first post according to my reading of it seemed to imply that the force of the wall onto the fluid was contributing or the sole factor in increasing the velocity of the flow through the contraction, which is not the case since the resultant force is against the flow, and that this is in part what causes the head loss inherent in a contraction. If that is not what you were implying, then I apologize.

Yes. Thanks Boneh3ad. I realized just before I went to bed last night that the axial component of the force the contraction wall exerts on the fluid acts in the direction opposite to the flow, rather than in the same direction. Sorry for that mistake. So, there are three forces that contribute to the acceleration of the fluid between points 1 and 2: the upstream pressure force (which acts in the direction of flow), the downstream pressure force (which acts opposite to the direction of flow), and the axial component of the force at the contraction (which also acts opposite to the direction of flow). The net of these three forces is in the direction of flow, and causes the fluid to accelerate.

 

[Chestermiller]

Although your conclusion is correct, your explanation does not seem to be, or I do not understand it. Force due to the wall of the pipe (in the friction-less case) cannot provide energy to the fluid if the wall does not move. The only effect of the force of the wall in such case is to curve the trajectories of the fluid particles. Their acceleration is due to the forces of the other fluid particles, since there is a gradient of pressure in the fluid.

This is not correct. The converging wall exerts a force on the fluid, and this force has a component in the axial direction. The force of the wall can certainly affect the energy of the fluid (i.e., do work on the fluid) even if the wall does not move because there is relative movement between the fluid at the wall and the wall itself. In the case of an ideal fluid (i.e., zero viscosity fluid) like the situation here, the no-slip boundary condition does not have to be satisfied at the wall.

 

[Jano L.]

The force of the wall can certainly affect the energy of the fluid (i.e., do work on the fluid) even if the wall does not move because there is relative movement between the fluid at the wall and the wall itself.

This is not correct. The work done by the force of the wall upon the fluid is given by

$$
F\Delta s \cos \varphi,
$$

where $F$ is the magnitude of the force, $\Delta s$ is the displacement of the fluid element and $\varphi$ is the angle between the direction of the force and the direction of the displacement. Since the fluid in contact with the wall moves along the wall, the angle is equal to 90° and the cosine vanishes.

The fluid elements farther from the wall do not move exactly along the wall, but they are not in contact with it anymore, so they do not experience force from it. They experience force due to other fluid elements only (gradient forces).

 

[Chestermiller]

This is not correct. The work done by the force of the wall upon the fluid is given by

$$
F\Delta s \cos \varphi,
$$

where $F$ is the magnitude of the force, $\Delta s$ is the displacement of the fluid element and $\varphi$ is the angle between the direction of the force and the direction of the displacement. Since the fluid in contact with the wall moves along the wall, the angle is equal to 90° and the cosine vanishes.

The fluid elements farther from the wall do not move exactly along the wall, but they are not in contact with it anymore, so they do not experience force from it. They experience force due to other fluid elements only (gradient forces).

Oops. You're absolutely right. Sorry. My mistake.

However, we should still make it clear that the pressure force exerted by the converging wall does exert a force with a component in the axial direction on the fluid, and this figures in the macroscopic axial force balance on the fluid.

Chet

 

[tiny-tim]

and i see that ultimately, it's the magnitude of that sideways external force which is providing the extra energy (pressure = energy density), and it's providing more extra energy behind me than in front of me because the pipe is providing more sideways external force where it's wider

Force due to the wall of the pipe (in the friction-less case) cannot provide energy to the fluid if the wall does not move.

of course, you're correct: the energy in the pipe is constant, so energy is certainly not being provided!

i should have written:​

so i look sideways, and i see that the molecules closer to the pipe are pushing the molecules closer to the centre, all the way back to the pipe itself, where the pipe itself (it's not its fault, it can't help it!) is providing the only other external force, a sideways (and partly backwards) one

and i see that ultimately, it's the magnitude of that sideways external force which is providing the extra longitudinal force on me, and it's providing more extra force behind me than in front of me because the magnitude of that external force is greater where the pipe is wider

(and my increase in energy is caused by the greater work done on me by the greater force behind me than by the lesser force in front of me)​

 

[Jano L.]

Oops. You're absolutely right. Sorry. My mistake.

However, we should still make it clear that the pressure force exerted by the converging wall does exert a force with a component in the axial direction on the fluid, and this figures in the macroscopic axial force balance on the fluid.

Chet

No problem, we all make mistakes. The pipe or container certainly exerts force on the fluid when it moves, and it is sometimes useful to consider this force, for example when estimating the efflux coefficient (see the Feynman Lectures, vol. II, sec. 40-3), or when calculating the reaction on the pipe itself.