BigFlorida
- 41
- 1
I have a multivariable function z = x2 + 2y2 such that x = rcos(t) and y = rsin(t). I was asked to find
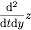 (I know the d's should technically be curly, but I am not the best at LaTeX). I thought this would just be a simple application of chain rule:
(I know the d's should technically be curly, but I am not the best at LaTeX). I thought this would just be a simple application of chain rule:
∂2/(∂y∂t) = (∂z/∂x)(ⅆx/ⅆt) + (∂z/∂y)(ⅆy/ⅆt)
but apparently this is not the case. Could someone perhaps explain why this is not the right thing to do. When I did it this way I got 2x = 2rcos(t) = 2ycot(t) as my answer, but my book says the answer is -2y2cot(t)csc2(t) and I have no clue what they are doing.
Any help would be appreciated. Thank you in advance.
∂2/(∂y∂t) = (∂z/∂x)(ⅆx/ⅆt) + (∂z/∂y)(ⅆy/ⅆt)
but apparently this is not the case. Could someone perhaps explain why this is not the right thing to do. When I did it this way I got 2x = 2rcos(t) = 2ycot(t) as my answer, but my book says the answer is -2y2cot(t)csc2(t) and I have no clue what they are doing.
Any help would be appreciated. Thank you in advance.