tracker890 Source h
- 90
- 11
- Homework Statement
- Determine flow rate per unite width in the line
- Relevant Equations
- flow rate equation
Q:Please hlep me to understand which ans is correct.To determine the flow rate in Line AB.
$$\mathrm{Known}:V_A,q,r_A = constant.$$

so/
select:## A,{B}^{\text{'}},B,A,## is control volume
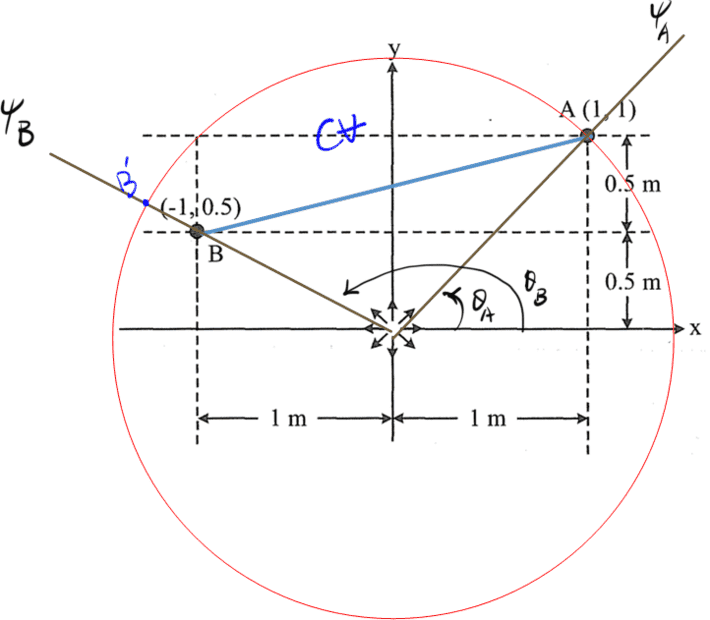
$${Q}_{AB}={Q}_{A{B}^{\text{'}}}=\iint _{A}^{}({V}_{A})dA={\int }_{{\theta }_{A}}^{{\theta }_{B}}({V}_{A}){r}_{A}d\theta $$$$\overset\rightharpoonup{V}=\triangledown \phi =<\frac{\partial \phi }{\partial r},\frac{1}{r}\frac{\partial \phi }{\partial \theta }>=<\frac{1}{r}\frac{\partial \psi }{\partial \theta },-\frac{\partial \psi }{\partial r}>=<{V}_{r},{V}_{\theta }> $$$$\therefore V_A=\frac1{r_A}\frac{\partial\psi}{\partial\theta}\;$$$$Q_{AB}=\int_{\theta_A}^{\theta_B}{(V_A)}r_Ad\theta\;=\;\int_{\theta_A}^{\theta_B}{(\frac1{r_A}\frac{\partial\psi}{\partial\theta})}r_Ad\theta=\int_{\theta_A}^{\theta_B}{(\frac{\partial\psi}{\partial\theta})}d\theta=\psi_B-\psi_A$$to find ##\psi##,
$$F(z)=\frac q{2\pi}\ln(z)=\frac q{2\pi}ln(re^{i\theta})=\frac q{2\pi}\ln r+i\frac q{2\pi}\theta=\phi+i\psi$$so $$\psi=\frac q{2\pi}\theta$$
$$Q_{AB}=\psi\left(\theta_B\right)\mathit-\psi\left(\theta_A\right)\mathit=\frac q{2\pi}(\theta_B-\theta_A)$$$$\theta_A=\tan^{-1}\left(\frac11\right)=0.7854\;rad,$$
$$\theta_B=\frac\pi2+\tan^{-1}\left(\frac1{0.5}\right)=2.6779\;rad$$
So ans by myself is
$$\therefore Q_{AB}=\frac q{2\pi}{(2.6779-0.7854)}=0.3012q............(Ans(1))$$$$////////////////////////$$
But book say:
$$\theta_A=\tan^{-1}\left(\frac yx\right)=\tan^{-1}\left(\frac{\mathit1}{\mathit1}\right)=0.7854\;rad$$$$\theta_B=\tan^{-1}\left(\frac yx\right)=\tan^{-1}\left(\frac{0.5}{-1}\right)\;=\;-0.4636\;rad$$$$Q_{AB}=\psi\left(\theta_A\right)-\psi\left(\theta_B\right)=\frac q{2\pi}{(0.7854+0.4636)}=0.19878q........(Ans(2))$$
$$\mathrm{Known}:V_A,q,r_A = constant.$$
so/
select:## A,{B}^{\text{'}},B,A,## is control volume
$${Q}_{AB}={Q}_{A{B}^{\text{'}}}=\iint _{A}^{}({V}_{A})dA={\int }_{{\theta }_{A}}^{{\theta }_{B}}({V}_{A}){r}_{A}d\theta $$$$\overset\rightharpoonup{V}=\triangledown \phi =<\frac{\partial \phi }{\partial r},\frac{1}{r}\frac{\partial \phi }{\partial \theta }>=<\frac{1}{r}\frac{\partial \psi }{\partial \theta },-\frac{\partial \psi }{\partial r}>=<{V}_{r},{V}_{\theta }> $$$$\therefore V_A=\frac1{r_A}\frac{\partial\psi}{\partial\theta}\;$$$$Q_{AB}=\int_{\theta_A}^{\theta_B}{(V_A)}r_Ad\theta\;=\;\int_{\theta_A}^{\theta_B}{(\frac1{r_A}\frac{\partial\psi}{\partial\theta})}r_Ad\theta=\int_{\theta_A}^{\theta_B}{(\frac{\partial\psi}{\partial\theta})}d\theta=\psi_B-\psi_A$$to find ##\psi##,
$$F(z)=\frac q{2\pi}\ln(z)=\frac q{2\pi}ln(re^{i\theta})=\frac q{2\pi}\ln r+i\frac q{2\pi}\theta=\phi+i\psi$$so $$\psi=\frac q{2\pi}\theta$$
$$Q_{AB}=\psi\left(\theta_B\right)\mathit-\psi\left(\theta_A\right)\mathit=\frac q{2\pi}(\theta_B-\theta_A)$$$$\theta_A=\tan^{-1}\left(\frac11\right)=0.7854\;rad,$$
$$\theta_B=\frac\pi2+\tan^{-1}\left(\frac1{0.5}\right)=2.6779\;rad$$
So ans by myself is
$$\therefore Q_{AB}=\frac q{2\pi}{(2.6779-0.7854)}=0.3012q............(Ans(1))$$$$////////////////////////$$
But book say:
$$\theta_A=\tan^{-1}\left(\frac yx\right)=\tan^{-1}\left(\frac{\mathit1}{\mathit1}\right)=0.7854\;rad$$$$\theta_B=\tan^{-1}\left(\frac yx\right)=\tan^{-1}\left(\frac{0.5}{-1}\right)\;=\;-0.4636\;rad$$$$Q_{AB}=\psi\left(\theta_A\right)-\psi\left(\theta_B\right)=\frac q{2\pi}{(0.7854+0.4636)}=0.19878q........(Ans(2))$$
Last edited: