Question for Kirchhoff's current law for RC circuit

[goodphy]

Hello.

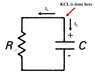
Maybe this is very basic and important question for circuit analysis. Please see the attached image.

KCL (Kirchhoff's Current Law) is applied to red arrow-indicated point and I choose the convention that current flowing out from the point is positive.

- side of the capacitor is actually grounded thus its voltage is 0 and red arrow point is V.

I₁ = V/R and I₂ = C(dV/dt).

Substituting these to KCL as I₁ + I₂ = 0 give the right equation as

V/R + C(dV/dt) = 0

The solution of exponentially decaying with time constant of RC.

Until this problem is solved well. Good!

But what if I choose the direction of I₂ in opposite way? In this case KCL becomes

V/R - C(dV/dt) = 0

and solution is not right. V increases forever!

Only solution to solve this problem is to accept the idea that C(dV/dt) is positive only when current is from + to - through the capacitor. But why? The current can go + to - in rounding circuit all the way. (It is counter-clock wise direction here.)

Could you tell me why i = C(dV/dt) has positive polarity only when current is across the capacitor from + to negative? Is there any physical reason?

 

[Svein]

Entropy. The capacitor will not fill itself with charge, it wants to return to the no-charge state. Therefore, the direction of current must indicate the emptying of capacitor charge.

 

[Dale]

But what if I choose the direction of I2 in opposite way? In this case KCL becomes

V/R - C(dV/dt) = 0

and solution is not right. V increases forever!

If you change the direction of I2 then the voltage across the capacitor is -V. So your equation would be V/R - C(d(-V)/dt) = 0 which is the same as the correct equation V/R + C(dV/dt) = 0.

But don't ever do that. You will just confuse yourself and lead to mistakes. Adopt the standard convention and use it consistently every time.

 

[Hesch]

V/R - C(dV/dt) = 0

Well, choosing the opposite direction as for the arrow I2, you will change sign of your result.

1A in the first direction = -1A in the opposite direction.

So the physical current will not change its positive direction. If you (also) change direction of the arrow as for I1, you will get the equation:

-V/R - C(dV/dt) = 0

 

[goodphy]

Thanks for replaying, people. I've been encouraged to imagine which current direction should be taken when empty capacitor is connected with the battery then I understood that this convention is actually true.

 

[Dale]

I understood that this convention is actually true.

Well, conventions are not about being true or false, they are about being consistent. As long as you are consistent you will get the right answer.

So we adopt the conventions and apply them the exact same way each and every time, not because they are true, but for consistency.