- #1
Kaushik
- 282
- 17
Consider a circuit with a witch, capacitor and an AC voltage source.
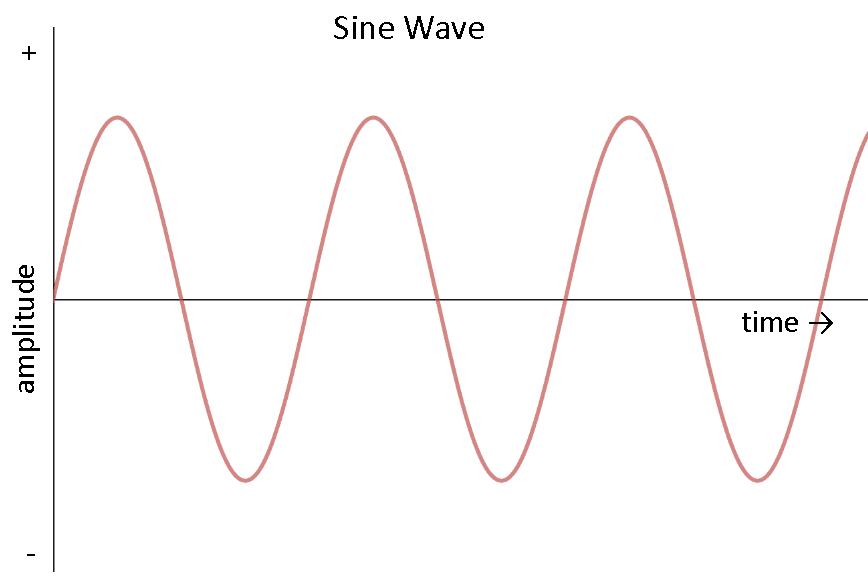
The sinusoidal AC voltage source is depicted in the following graph:
We know that, ##Q = CV##
##\frac{dQ}{dt} = C \frac{dV}{dt}##
##i = C\frac{dV}{dt} \tag{1}##
So from the graph, the voltage increases rapidly around ## t = 0##.
So, as ##\frac{dV}{dt}## is high (but ##V = 0##), ##i## must also be high.
Similarly, when ##V## attains a maximum, ##\frac{dV}{dt}=0##. Hence, ##i = 0##.
So we can see that current is ahead of voltage by ##\pi/2##.
But, I can't feel it. Could someone please give an intuitive explanation to this?
The sinusoidal AC voltage source is depicted in the following graph:
We know that, ##Q = CV##
##\frac{dQ}{dt} = C \frac{dV}{dt}##
##i = C\frac{dV}{dt} \tag{1}##
So from the graph, the voltage increases rapidly around ## t = 0##.
So, as ##\frac{dV}{dt}## is high (but ##V = 0##), ##i## must also be high.
Similarly, when ##V## attains a maximum, ##\frac{dV}{dt}=0##. Hence, ##i = 0##.
So we can see that current is ahead of voltage by ##\pi/2##.
But, I can't feel it. Could someone please give an intuitive explanation to this?
Last edited by a moderator: