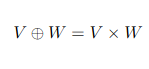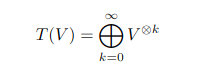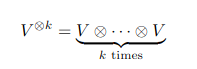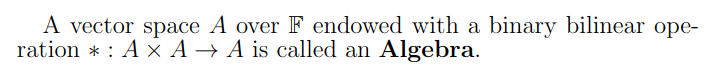Question Regarding Definition of Tensor Algebra

[jv07cs]

I am currently reading this book on multilinear algebra ("Álgebra Linear e Multilinear" by Rodney Biezuner, I guess it only has a portuguese edition) and the book defines an Algebra as follows:

It also defines the direct sum of two vector spaces, let's say V and W, as the cartesian product V x W:

Later on, it defines the Tensor Algebra of V, let's call it T(V) as:

Where

If the tensor product is the binary operation of the algebra T(V), it would have to act on the n-tuples of the cartesian product of all these tensor spaces? What would the tensor product between n-tuples mean? I am quite confused about this.

 

[fresh_42]

The binary algebra multiplication on $T(V)$ is
$$
(v_1\otimes v_2\otimes \ldots\otimes v_n )\cdot (w_1\otimes w_2\otimes \ldots\otimes w_m )=v_1\otimes v_2\otimes \ldots\otimes v_{n}\otimes w_1\otimes w_2\otimes \ldots\otimes w_m
$$
You get all other multiplications by the distributive law, e.g.
$$
(v_1\otimes v_2) \cdot (v_1+v_2\otimes v_4\otimes v_{17})=v_1\otimes v_2\otimes v_1+v_1\otimes v_2\otimes v_2\otimes v_4\otimes v_{17} \quad (*)
$$
This is literally a universal property. Things become interesting if we add more rules, e.g. if we define $v\otimes v =0$ and $v\otimes w=w\otimes v$ as in a Graßmann algebra. In that case, the tensor in $(*)$ would be zero.

Here is an overview of the main algebras:
https://www.physicsforums.com/insights/introduction-to-the-world-of-algebras/

 

[jv07cs]

The binary algebra multiplication on $T(V)$ is
$$
(v_1\otimes v_2\otimes \ldots\otimes v_n )\cdot (w_1\otimes w_2\otimes \ldots\otimes w_m )=v_1\otimes v_2\otimes \ldots\otimes v_{n}\otimes w_1\otimes w_2\otimes \ldots\otimes w_m
$$
You get all other multiplications by the distributive law, e.g.
$$
(v_1\otimes v_2) \cdot (v_1+v_2\otimes v_4\otimes v_{17})=v_1\otimes v_2\otimes v_1+v_1\otimes v_2\otimes v_2\otimes v_4\otimes v_{17} \quad (*)
$$
This is literally a universal property. Things become interesting if we add more rules, e.g. if we define $v\otimes v =0$ and $v\otimes w=w\otimes v$ as in a Graßmann algebra. In that case, the tensor in $(*)$ would be zero.

Here is an overview of the main algebras:
https://www.physicsforums.com/insights/introduction-to-the-world-of-algebras/

Thank you very much for the reply.

I am confused because, using that definition $\cdot: T(V) \times T(V) \rightarrow T(V)$ for the binary multiplication, this multiplication would have to act on elements of $T(V)$, which, using that definition of the direct sum as the cartesian product, would be n-tuples $(a, v, v_1 \otimes v_2, \dots)$ where $a \in \mathbb{F}$, $v \in V$, $v_1 \otimes v_2 \in V\otimes V$.

So if the binary multiplication acts on elements of $T(V)$, we would have something like $(a, v, v_1 \otimes v_1, \dots) \cdot (b, w, w_1 \otimes w_2, \dots)$, right? My question is then if there is a problem with the definition I'm using for the binary operation or even for the definition of the direct sum?

 

[fresh_42]

Thank you very much for the reply.

I am confused because, using that definition $\cdot: T(V) \times T(V) \rightarrow T(V)$ for the binary multiplication, this multiplication would have to act on elements of $T(V)$, which, using that definition of the direct sum as the cartesian product, would be n-tuples $(a, v, v_1 \otimes v_2, \dots)$ where $a \in \mathbb{F}$, $v \in V$, $v_1 \otimes v_2 \in V\otimes V$.

So if the binary multiplication acts on elements of $T(V)$, we would have something like $(a, v, v_1 \otimes v_1, \dots) \cdot (b, w, w_1 \otimes w_2, \dots)$, right? My question is then if there is a problem with the definition I'm using for the binary operation or even for the definition of the direct sum?

Yes and no. It becomes more transparent if you write the elements of the tensor algebra as sums instead of tuples. It is the same ...
$$
(a, v, v_1 \otimes v_2, \dots) = \sum_{n=0}^\infty a_n \cdot v^{(n)}_1\otimes \ldots\otimes v^{(n)}_n \text{ with only finitely many } a_n\neq 0
$$
... where I used $a=a_0$ here but the sum has the advantage that the distributive law kicks in more naturally
\begin{align*}
\left(\sum_{n=0}^\infty a_n \cdot v^{(n)}_1\otimes \ldots\otimes v^{(n)}_n\right) &\cdot\left(\sum_{m=0}^\infty b_m \cdot w^{(m)}_1\otimes \ldots\otimes w^{(m)}_m\right)\\&=
\sum_{k=0}^\infty \sum_{n+m=k} a_nb_m v^{(n)}_1\otimes\ldots\otimes v^{(n)}_n\otimes w^{(m)}_1\otimes \ldots\otimes w^{(m)}_m
\end{align*}
Elements of the tensor algebra are the linear span of $\{\mathbb{F}\, , \,V\, , \,V\otimes V\, , \,V\otimes V\otimes V\, , \,\ldots\}.$ But as you can see on the formula for an arbitrary multiplication, it is a bit messy. So people often only mention multiplications between $v_1\otimes \ldots \otimes v_n$ and $w_1\otimes \ldots \otimes w_m$ since the distributive law contributes all the other multiplications.

A tensor algebra is a so-called graded algebra $T(V)=\bigoplus_{n=0}^\infty V^{\otimes n}$ with the convention that $V^{\otimes 0}=\mathbb{F}.$ Multiplications are defined
$$
V^{\otimes n} \, \times \,V^{\otimes m} \longrightarrow V^{\otimes (n+m)}\, , \,(v_1\otimes \ldots \otimes v_n\, , \,w_1\otimes \ldots \otimes w_m)\longmapsto v_1\otimes \ldots \otimes v_n\otimes w_1\otimes \ldots \otimes w_m
$$
plus the distributive law. The multiplication is simply another tensor product, shifting a first factor of degree $n$ and a second factor of degree $m$ to a combined tensor of degree $n+m$. Plus distributive law for all general cases.

A tensor algebra is a huge construction. It is often used as the first step. The second would be the consideration of an ideal $\mathcal{I}(V)$ in the tensor algebra. The third step is then the consideration of the factor algebra (or quotient algebra, both names can be found in the literature) $T(V)/\mathcal{I}(V).$ It means that the elements in the ideal are considered to be zero, i.e. we implemented additional rules. These additional rules can make $T(V)/\mathcal{I}(V)$ finite-dimensional - note that $T(V)$ is infinite-dimensional - it can make $T(V)/\mathcal{I}(V)$ a Graßman algebra or a Lie algebra, depending on how we define $\mathcal{I}(V).$

 

[jv07cs]

Yes and no. It becomes more transparent if you write the elements of the tensor algebra as sums instead of tuples. It is the same ...
$$
(a, v, v_1 \otimes v_2, \dots) = \sum_{n=0}^\infty a_n \cdot v^{(n)}_1\otimes \ldots\otimes v^{(n)}_n \text{ with only finitely many } a_n\neq 0
$$
... where I used $a=a_0$ here but the sum has the advantage that the distributive law kicks in more naturally
\begin{align*}
\left(\sum_{n=0}^\infty a_n \cdot v^{(n)}_1\otimes \ldots\otimes v^{(n)}_n\right) &\cdot\left(\sum_{m=0}^\infty b_m \cdot w^{(m)}_1\otimes \ldots\otimes w^{(m)}_m\right)\\&=
\sum_{k=0}^\infty \sum_{n+m=k} a_nb_m v^{(n)}_1\otimes\ldots\otimes v^{(n)}_n\otimes w^{(m)}_1\otimes \ldots\otimes w^{(m)}_m
\end{align*}
Elements of the tensor algebra are the linear span of $\{\mathbb{F}\, , \,V\, , \,V\otimes V\, , \,V\otimes V\otimes V\, , \,\ldots\}.$ But as you can see on the formula for an arbitrary multiplication, it is a bit messy. So people often only mention multiplications between $v_1\otimes \ldots \otimes v_n$ and $w_1\otimes \ldots \otimes w_m$ since the distributive law contributes all the other multiplications.

A tensor algebra is a so-called graded algebra $T(V)=\bigoplus_{n=0}^\infty V^{\otimes n}$ with the convention that $V^{\otimes 0}=\mathbb{F}.$ Multiplications are defined
$$
V^{\otimes n} \, \times \,V^{\otimes m} \longrightarrow V^{\otimes (n+m)}\, , \,(v_1\otimes \ldots \otimes v_n\, , \,w_1\otimes \ldots \otimes w_m)\longmapsto v_1\otimes \ldots \otimes v_n\otimes w_1\otimes \ldots \otimes w_m
$$
plus the distributive law. The multiplication is simply another tensor product, shifting a first factor of degree $n$ and a second factor of degree $m$ to a combined tensor of degree $n+m$. Plus distributive law for all general cases.

A tensor algebra is a huge construction. It is often used as the first step. The second would be the consideration of an ideal $\mathcal{I}(V)$ in the tensor algebra. The third step is then the consideration of the factor algebra (or quotient algebra, both names can be found in the literature) $T(V)/\mathcal{I}(V).$ It means that the elements in the ideal are considered to be zero, i.e. we implemented additional rules. These additional rules can make $T(V)/\mathcal{I}(V)$ finite-dimensional - note that $T(V)$ is infinite-dimensional - it can make $T(V)/\mathcal{I}(V)$ a Graßman algebra or a Lie algebra, depending on how we define $\mathcal{I}(V).$

So the summation representation in the direct sum is just a way to represent the tuples, but the addition of elements still works in the component-wise manner of the tuple representation, where we only add elements of the same vector space, since we can't add tensors of different type, right?

If so, I would then have just three more questions:

1. In way, would it be correct to state that the binary operation $\cdot: T(V)\times T(V) \rightarrow T(V)$ is not exactly the tensor product (as previously defined by a bilinear map that takes elements of a space of (p,q)-tensors and elements of a space of (m,r)-tensors and returns elements of a space of (p+m,q+r)-tensors), but is more specifically a binary operation that kind of distributes the already defined tensor product?
2. Are the elements of $T(V)$ tensors? And what is the need in defining the vector space $T(V)$? Is it just a way to kind of reunite in a single set all tensors?
3. The algebra $T(V)$ only deals with contravariant tensors and we could define a $T(V^*)$ algebra that deals with covariant tensors. Is there an algebra that deals with both?

 

[fresh_42]

So the summation representation in the direct sum is just a way to represent the tuples, but the addition of elements still works in the component-wise manner of the tuple representation, where we only add elements of the same vector space, since we can't add tensors of different type, right?

Not sure what you mean. We can add tensors of different types formally: $(a)+ (u\otimes v)=a+u\otimes v.$ Whether you write them as tuples or as sums don't make a difference. But since we are dealing with vector spaces, sums are the preferred choice. Here are two examples written both ways:
\begin{align*}
(a,u,v\otimes w)+(b,u',v'\otimes w')&=(a+b,u+u',v\otimes w+v'\otimes w')\\
a+u+v\otimes w + b+u'+v'\otimes w'&=(a+b)+(u+u')+(v\otimes w+v'\otimes w')\\
(0,0,u\otimes v\otimes w) + (b,0,u\otimes v\otimes z)&=(b,0,u\otimes v\otimes (w+z))\\
u\otimes v\otimes w+b+u\otimes v\otimes z &=b+u\otimes v\otimes (w+z)
\end{align*}
See, there is another reason to use sums. You do not expect sums to be infinitely long, but the tuples that I wrote as finite tuples should be filled up with infinitely many zeros. If you write them as infinite sums, then you must add that only finitely many terms are unequal zero. If you have a specific tensor, then you can just use finite sums. If you use finite tuples, then you have always to count the position and that is a source of mistakes.

If so, I would then have just three more questions:

1. In way, would it be correct to state that the binary operation $\cdot: T(V)\times T(V) \rightarrow T(V)$ is not exactly the tensor product (as previously defined by a bilinear map that takes elements of a space of (p,q)-tensors and elements of a space of (m,r)-tensors and returns elements of a space of (p+m,q+r)-tensors), but is more specifically a binary operation that kind of distributes the already defined tensor product?

You shouldn't speak of $(p,q)$ tensors this way because it has a different meaning, especially for physicists and I am not sure which meaning you use here.

If we have a tensor of degree $p$ and a tensor of degree $q$, then their multiplication is the tensor product. It has degree $p+q.$ This is the multiplication is $T(V).$ It has to obey the distributive law, the sums of tensors are formal sums, the product of tensors is the tensor product of those tensors.

If you mean a $(p,q)$ tensor as physicists use it, namely as an element of the vector space
$$
\underbrace{V^*\otimes \ldots V^*}_{p-\text{times}} \otimes \underbrace{V\otimes \ldots\otimes V}_{q-\text{times}}
$$
then we speak actually about the tensor algebra $T(V^*)\otimes T(V)\cong T(V^*\otimes V).$ The multiplication of tensors of degree $(p,q)$ with tensors of degree $(r,m)$ is then again a tensor product, one of degree $(p+r,q+m)$ with a rearrangment such that all vectors from $V^*$ are grouped on the left.

1. Are the elements of $T(V)$ tensors?

Yes.

1. And what is the need in defining the vector space $T(V)$? Is it just a way to kind of reunite in a single set all tensors?

For one, yes. It contains all multiples and (formal) sums of pure tensors $v_1\otimes \ldots\otimes v_n.$

The sense is what I described above. Physicists encounter tensors from the tensor algebra $T(V^*)\otimes T(V)$ like e.g. curvature tensors, and also Graßmann and Lie algebras that are obtained by the procedure I described in post #4 via the ideals. The universality of the tensor algebra grants many applications with different sets of additional rules expressed in the vectors that span the ideal $\mathcal{I}(V)$ I spoke of in post #4.

The word tensor is normally used very sloppy. People often mean pure tensors like $a\otimes b$ and forget that $a\otimes b +c\otimes d$ is also a tensor of the same degree. Then they say tensor when they mean a general tensor from $T(V)$ with multiple components of different degrees and sums thereof, or if they mean a tensor from $T(V^*)\otimes T(V).$ They always say tensor.

1. The algebra $T(V)$ only deals with contravariant tensors and we could define a $T(V*)$ algebra that deals with covariant tensors. Is there an algebra that deals with both?

Yes, see above, $T(V^*)\otimes T(V)\cong T(V^*\otimes V).$ Maybe I confused the order when I wrote about a $(p,q)$ tensor. Not sure, what you call co- and what contravariant, and what comes left and what on the right side. That's a physical thing. There is no mathematical necessity to name them. And if that wasn't already confusing, the terms co- and contravariant are used differently in mathematics. It is a historical issue.

 

[mathwonk]

just think of them as non commutative polynomials. so a product of elements of degree p and degree q has degree p+q.

as for mixed tensors, note that V*tensV ≈ Hom(V,V). so it is nothing new.

 

[jv07cs]

Not sure what you mean. We can add tensors of different types formally: (a)+(u⊗v)=a+u⊗v. Whether you write them as tuples or as sums don't make a difference. But since we are dealing with vector spaces, sums are the preferred choice. Here are two examples written both ways:

Oh ok. Just to make sure I don't misunderstand it, a formal sum of two tensors would just be a way to combine two tensors but without necessarily implying any operation or computation? I am asking this because I don't know if I really understand the concept of formal sum.

(a,u,v⊗w)+(b,u′,v′⊗w′)=(a+b,u+u′,v⊗w+v′⊗w′)a+u+v⊗w+b+u′+v′⊗w′=(a+b)+(u+u′)+(v⊗w+v′⊗w′)(0,0,u⊗v⊗w)+(b,0,u⊗v⊗z)=(b,0,u⊗v⊗(w+z))u⊗v⊗w+b+u⊗v⊗z=b+u⊗v⊗(w+z)
See, there is another reason to use sums. You do not expect sums to be infinitely long, but the tuples that I wrote as finite tuples should be filled up with infinitely many zeros. If you write them as infinite sums, then you must add that only finitely many terms are unequal zero. If you have a specific tensor, then you can just use finite sums. If you use finite tuples, then you have always to count the position and that is a source of mistakes.

Yeah, I see how using sums is more advantageous. It makes sense.

If you mean a (p,q) tensor as physicists use it, namely as an element of the vector space
V∗⊗…V∗⏟p−times⊗V⊗…⊗V⏟q−times

That is exactly what I meant by (p,q)-tensor.

Yes.

The definition I am using of tensors is the one as a multilinear map $T: V^{*p}\times V^q \rightarrow \mathbb{F}$, which defines a tensor of type (p,q) and the set of all this tensors forms a vector space $\tau^{(p,q)}(V)$. From this definition, I don't see how the formal sum of two tensors generates a tensor. How would this multilinear map be defined?

 

[fresh_42]

Oh ok. Just to make sure I don't misunderstand it, a formal sum of two tensors would just be a way to combine two tensors but without necessarily implying any operation or computation? I am asking this because I don't know if I really understand the concept of formal sum.

You just write a sum. You cannot calculate vectors of different degrees because they "live" in different vector spaces. $a\in \mathbb{F}$ is a scalar, $w\in V$ is a vector and $u\otimes v \in \mathbb{M}(n,\mathbb{R})$ is a matrix of rank one. You cannot add these. However, $a+w+u\otimes v$ is an element of $T(V)$ and as such a tensor. Whether such things occur in real life is another question. Here is an example of how $2\times 2$ matrix multiplication can be expressed as a tensor which is a sum of seven triads $u^*\otimes v^*\otimes w.$
https://www.physicsforums.com/insights/what-is-a-tensor/
This means multiplication in $\mathbb{M}(2,\mathbb{R})$ can be performed with seven instead of eight generic multiplications.

The definition I am using of tensors is the one as a multilinear map $T: V^{*p}\times V^q \rightarrow \mathbb{F}$, which defines a tensor of type (p,q) and the set of all this tensors forms a vector space $\tau^{(p,q)}(V)$. From this definition, I don't see how the formal sum of two tensors generates a tensor. How would this multilinear map be defined?

Look at the example of Strassen's algorithm of matrix multiplication in the article I linked. This should answer your question.

(If you use a Tex-editor at home like me, then I can give you the formulas of that algorithm in Tex. Or you use a tex-extension in your browser and right-click on the formula with "Show Math as tex commands" to copy it to the computer's clipboard.)

Things become a little bit more complicated if we speak about the usage of tensors in physics. Multilinear implies flatness. Linear isn't curved. Yet, physicists speak about curvature tensors. However, this should be discussed in a separate thread. It involves analysis and differentiation which makes it a bit more complicated.

 

[jv07cs]

You just write a sum. You cannot calculate vectors of different degrees because they "live" in different vector spaces. $a\in \mathbb{F}$ is a scalar, $w\in V$ is a vector and $u\otimes v \in \mathbb{M}(n,\mathbb{R})$ is a matrix of rank one. You cannot add these. However, $a+w+u\otimes v$ is an element of $T(V)$ and as such a tensor. Whether such things occur in real life is another question. Here is an example of how $2\times 2$ matrix multiplication can be expressed as a tensor which is a sum of seven triads $u^*\otimes v^*\otimes w.$
https://www.physicsforums.com/insights/what-is-a-tensor/
This means multiplication in $\mathbb{M}(2,\mathbb{R})$ can be performed with seven instead of eight generic multiplications.


Look at the example of Strassen's algorithm of matrix multiplication in the article I linked. This should answer your question.

Things become a little bit more complicated if we speak about the usage of tensors in physics. Multilinear implies flatness. Linear isn't curved. Yet, physicists speak about curvature tensors. However, this should be discussed in a separate thread. It involves analysis and differentiation which makes it a bit more complicated.

Thank you for the reference, I'll read through it. And thank you very much for all the replies, it helped a lot.

 

[fresh_42]

Thank you for the reference, I'll read through it. And thank you very much for all the replies, it helped a lot.

Tell me if you find mistakes

Note that tensor products can be written as matrix multiplications: Say we have $\vec{u}=(1,2,3)$ and $\vec{v}=(7,13,19).$ Then
\begin{align*}
\vec{u} \otimes \vec{v}&=(1,2,3)\otimes (7,13,19)=\begin{pmatrix}1\\2\\3 \end{pmatrix}\cdot\begin{pmatrix}7&13&19\end{pmatrix}\\
&=\begin{pmatrix}1\cdot 7&1\cdot 13&1\cdot 19\\ 2\cdot 7&2\cdot 13&2\cdot 19\\3\cdot 7&3\cdot 13&3\cdot 19\end{pmatrix}\\[8pt]
&=\begin{pmatrix}7&13&19\\ 14& 26& 38\\ 21&39&57\end{pmatrix}
\end{align*}