Questions about the workings of a phase locked loop

[Master1022]

Homework Statement

1) What is the point of having another (low-pass) filter $G_f (s)$ for $V_o$ after already passing the voltage through a low pass filter?
2) Is there any particular relationship between the bandwidth of the low pass filter and the locking range of the PLL?

Relevant Equations

LPF

Hi,

I had one or two questions about the operation of a PLL, which refer to the diagrams below - a control representation of the system and a diagram of the low pass filter circuit.

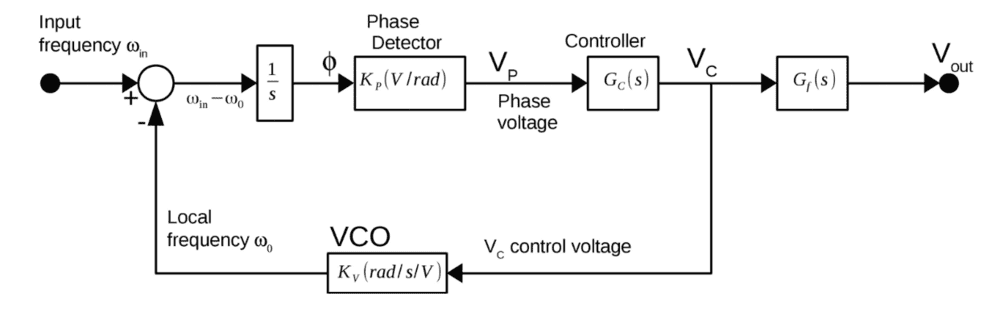
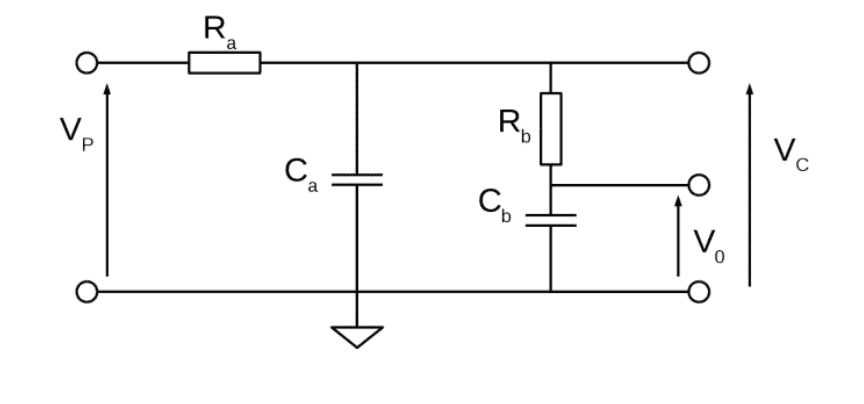
Questions:
1) What is the point of having another (low-pass) filter $G_f (s)$ for $V_o$ after already passing the voltage through a low pass filter?
I know that we want to filter the pulses output from the phase detector to form a voltage to input into the VCO. However, why is there another filter $G_f (s)$ that acts before the output $V_o$?

2) Is there any particular relationship between the bandwidth of the low pass filter and the locking range of the PLL?
I think I am slightly confused as to what these terms mean. Is the locking range the frequency range over which the PLL works (i.e. can detect signal frequencies between $x$ and $y$)? The bandwidth of the low pass filter determines the speed of response of the PLL?

Any help is greatly appreciated.

 

[DaveE]

1) What is the point of having another (low-pass) filter Gf(s) for Vo after already passing the voltage through a low pass filter?
I know that we want to filter the pulses output from the phase detector to form a voltage to input into the VCO. However, why is there another filter Gf(s) that acts before the output Vo?

I don't understand either. The PLL function ends at Vc, the frequency feedback. After all, you could disconnect Vo from Vc and you'd still have a perfectly functional PLL. You'll have to find the person that drew that block diagram and ask them. There are lots of reasons you may want to filter signals in a system, but you need to know about the system requirements to discuss those design aspects.

2) Is there any particular relationship between the bandwidth of the low pass filter and the locking range of the PLL?
I think I am slightly confused as to what these terms mean. Is the locking range the frequency range over which the PLL works (i.e. can detect signal frequencies between x and y)? The bandwidth of the low pass filter determines the speed of response of the PLL?

The capture range is the range of input frequencies that the PLL can sync with starting from the un-locked state.

The locking range is the range of input frequencies the loop can follow (stay locked to) after it has acquired lock within it's capture range. Of course, the locking range is always at least as large as the capture range.

The question about the effect of the loop filters is hard to answer. In general, that filter determines almost everything about how the loop works. So, yes, capture, lock, speed, all of it depends on the loop gain. Normally the phase detector and VCO are assumed to not really have any frequency dependence beyond the fundamental stuff they have to have, like phase being the integral of frequency.

edit: On second thought, the loop filter bandwidth is often irrelevant in determining the lock range, that usually has more to do with the VCO and phase detector or integrator ranges. The assumption is that the frequency is changed slowly when determining the locking range.

 

[Master1022]

Thank you @DaveE !

I don't understand either. The PLL function ends at Vc, the frequency feedback. After all, you could disconnect Vo from Vc and you'd still have a perfectly functional PLL. You'll have to find the person that drew that block diagram and ask them. There are lots of reasons you may want to filter signals in a system, but you need to know about the system requirements to discuss those design aspects.

Yes, I will try to find who has created that diagram.

The capture range is the range of input frequencies that the PLL can sync with starting from the un-locked state.

The locking range is the range of input frequencies the loop can follow (stay locked to) after it has acquired lock within it's capture range. Of course, the locking range is always at least as large as the capture range.

Okay, thanks. Do we say that the signal remains locked even if there is an instantaneous discrepancy between the reference and VCO output (due to the time the feedback loop takes)?

Follow up question relating to FM signal demodulation:
For FM modulation example above, the instantaneous frequency varies proportional to the message signal $f_{instantaneous} = f_{center} + ks(t)$ and $s(t)$ is the message signal. Just as a follow up to check my understanding, am I correct in thinking that $V_c$ (signal that feeds into VCO) is the signal that would track the information component in a frequency modulated signal? Would we want the center frequency of our to be in the capture range, whilst having the maximum and minimum frequencies $f_ {center} \pm k|s(t)_{max}|$ at least within the lock range?

The question about the effect of the loop filters is hard to answer. In general, that filter determines almost everything about how the loop works. So, yes, capture, lock, speed, all of it depends on the loop gain. Normally the phase detector and VCO are assumed to not really have any frequency dependence beyond the fundamental stuff they have to have, like phase being the integral of frequency.

edit: On second thought, the loop filter bandwidth is often irrelevant in determining the lock range, that usually has more to do with the VCO and phase detector or integrator ranges. The assumption is that the frequency is changed slowly when determining the locking range.

Okay that makes more sense.

 

[Fred Wright]

Is the reason for the final filter because the PLL can generate frequencies that are multiples (harmonics) of the input frequency? Just asking.

 

[DaveE]

Okay, thanks. Do we say that the signal remains locked even if there is an instantaneous discrepancy between the reference and VCO output (due to the time the feedback loop takes)?

Yes, within reasonable limits. If the PLL isn't locked you will see somewhat chaotic deviations in the VCO as the phase detector output varies greatly.

Would we want the center frequency of our to be in the capture range, whilst having the maximum and minimum frequencies fcenter±k|s(t)max| at least within the lock range?

I'm not sure, that's kind of a complicated question. I would guess that the PLL will lock ok. But, theoretically, you could have a DC signal that is outside of the capture range.

In practice the FM deviation is usually rather small so it is easy to have all of in within the capture range. In more sophisticated systems, people will adjust the bandwith/gain of the loop based on the locked/unlock status so an unlocked loop has wider bandwith. Then if you need the performance of a narrow bandwidth, you do that after the loop is locked.

 

[Master1022]

Thank you once again for your response.

Yes, within reasonable limits. If the PLL isn't locked you will see somewhat chaotic deviations in the VCO as the phase detector output varies greatly.

Okay cool.

One final question I have is what happens when the reference input frequency is outside of the PLL range? What does the output signal look like then?

 

[Master1022]

Thanks for your post @Fred Wright .

Is the reason for the final filter because the PLL can generate frequencies that are multiples (harmonics) of the input frequency? Just asking.

That's a good point. However, and please do correct me if I am wrong, I believe that requires there to be a frequency divider in the (feedback loop of the) control system/circuit. Unless the frequency divider is included in one of the elements, I don't think this particular circuit has that component.

 

[DaveE]

One final question I have is what happens when the reference input frequency is outside of the PLL range? What does the output signal look like then?

It's vary chaotic. Since the output of the phase detector is always changing. Phase detection only makes sense for signals with the same frequency.

Of course the loop filter plays a roll in this. If it is very slow then it may average the PD output somewhat, so VCO can't change as quickly or reach it's extreme values. But when the PLL is locked then the PD output can be more stable at extreme values which can then get through the loop filter. This is one reason why the capture range is smaller than the lock range. It also explains why you will sometimes see a PLL that captures an extreme input very slowly; the average VCO input isn't always in the center of the range and then will bias the PD output in turn. As the average VCO input moves, so does the capture range. It's a very complicated subject if you examine it closely.

 

[DaveE]

Is the reason for the final filter because the PLL can generate frequencies that are multiples (harmonics) of the input frequency? Just asking.

Maybe, but recall that the output in this case is the lower frequency (filtered) PD output/VCO input. The "baseband" not the "carrier". So, much of that filtering can be done in the loop filter. Still there may be filtering requirements that they don't want messing up their PLL feedback loop. For example many HF receivers offer FM in both "wide" and "narrow" modes. This is undoubtedly filtering after the PLL that tracks/demodulates the carrier. More related to downstream functions like AGC or audio output.

Anyway, it's not a generalized thing. It all depends on what sort of machine these guys want.

 

[Averagesupernova]

What they are calling the phase detector has only one input. Seems foreign to me.

 

[DaveE]

What they are calling the phase detector has only one input. Seems foreign to me.

Yes, the summer, integrator, and phase detector are all part of the same thing. But I do like that they explicitly show the integration function in the loop. That's the part that many don't understand.

There are different types of phase detectors, but the xor gate is one of the most common. It is a 1 bit summer, so these diagrams are often drawn this way. Maybe because it looks like conventional feedback systems?