mysci
- 9
- 0
We know the rule of cross product
Why here |absinΘ| =
Thanks for explanation.
|a||b|sinθ is the area of the base, and is also the magnitude of the cross product of ##\vec{a}## and ##\vec{b}## -- i.e., |##\vec{a}## X ##\vec{b}|##. |c|cosφ gives the height of the parallelipiped. The product of the area of the base and the height gives the volume of the cell.mysci said:View attachment 79881
We know the rule of cross productView attachment 79882 or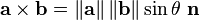
Why here |absinΘ| = View attachment 79883 , and View attachment 79884 = c cos Φ in the above picture?
Mark44 said:|a||b|sinθ is the area of the base, and is also the magnitude of the cross product of ##\vec{a}## and ##\vec{b}## -- i.e., |##\vec{a}## X ##\vec{b}|##. |c|cosφ gives the height of the parallelipiped. The product of the area of the base and the height gives the volume of the cell.
|a x b| is a scalar, while |a x b|n is a vector that points straight up, and that whose magnitude is the area of the base. If you dot this vector (|a x b|n) with c, you get the volume. One definition for the dot product of a and b is ##a \cdot b = |a| |b| cos(\theta)##, where ##\theta## is the angle between the two vectors. In your problem, the angle is ##\phi##.mysci said:Thanks.
Yes, but why not |axb|, is |axb|(unit vector n) in third step?
mysci said:absinΘ and |axbl are also magnitudes, but |axb|(unit vector n) is a vector. absinΘ = |axb| ≠ |axb|(unit vector n) = vector a x vector b.
However, here absinΘ = |axb|(unit vector n). I don't understand this.
On the other hand, ccosφ is the height of parallelogram, how to change it to vector c? I don't understand it as well.
Thanks.
Mark44 said:|a x b| is a scalar, while |a x b|n is a vector that points straight up, and that whose magnitude is the area of the base. If you dot this vector (|a x b|n) with c, you get the volume. One definition for the dot product of a and b is ##a \cdot b = |a| |b| cos(\theta)##, where ##\theta## is the angle between the two vectors. In your problem, the angle is ##\phi##.
Thanks.Mark44 said:I use LaTeX. Put either two # symbols at the front and two more at the end (for inline) or two $ symbols front and back (for standalone).
Here I'm adding an extra space between each pair so you can see what it looks like without being rendered: # #\vec{a}# #
Removing the spaces gives ##\vec{a}##
Should be |a||b|sinθ = |a x b|. a and b are vectors, so ab is not defined. Both sides of the equation should be scalars, which is why you have the magnitudes (absolute values).mysci said:Thanks.
Then
I got following,
absinΘ = |axb|
The right side is a scalar because it's a dot product, so the left side needs to be a scalar as well.mysci said:ccosΦ = n·c
mysci said:Is it right?
Thank you.Mark44 said:Should be |a||b|sinθ = |a x b|. a and b are vectors, so ab is not defined. Both sides of the equation should be scalars, which is why you have the magnitudes (absolute values).
The right side is a scalar because it's a dot product, so the left side needs to be a scalar as well.
The left side should be |c|cosΦ.