Samurai44
- 57
- 0
Greetings,
I have some questions about ln(x) and e^x graphs , with figuring out Domain , range and line of asymptote.
Q1) How can I know if this graph is ln(x) or e^x
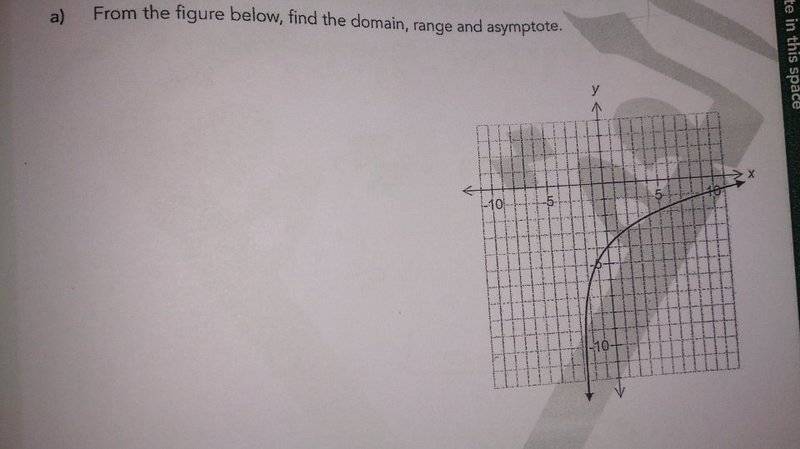
(I thought it was e^x graph since there's no x-axis intercept , however the answer in marking scheme is:
Domain : xεR , x>-3
Range : yεR
Ast. : x=-3
So it is ln(x) since there is a x-range/value in the domain .(correct me if i am wrong)
Q2) what's the difference between the two following two graphs ,, and how can I find the domain and range ?
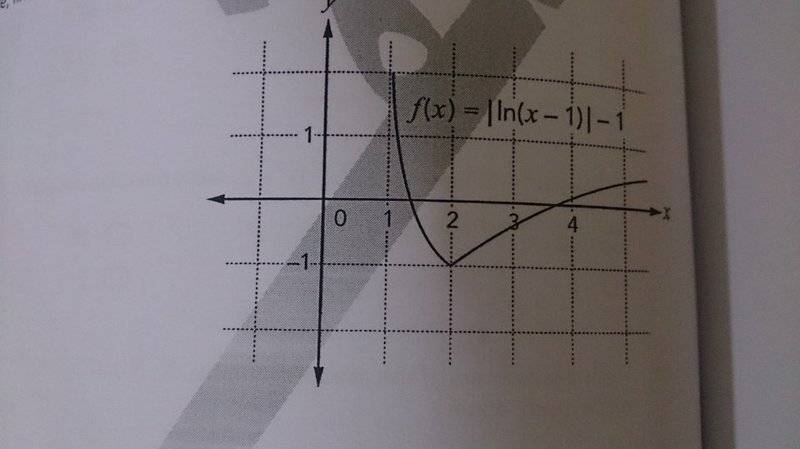
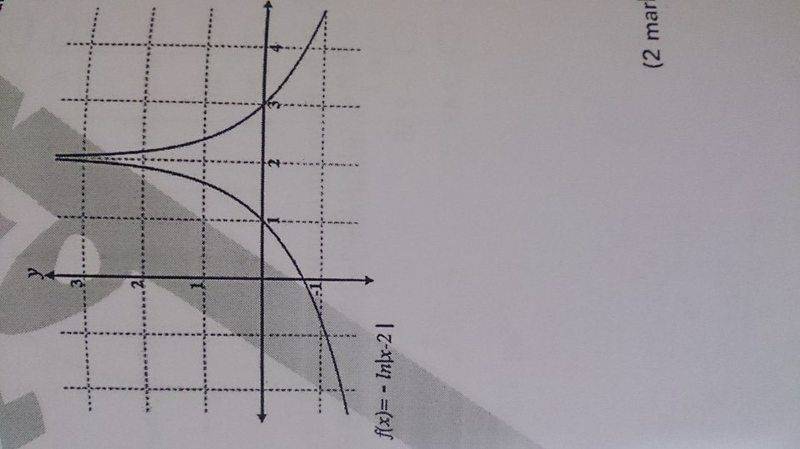
Its the Modulus function that confuses me and make it hard to get the domain value.
*No calculations are required from the above question, as it says "from the figure ... "
Thank you,
I have some questions about ln(x) and e^x graphs , with figuring out Domain , range and line of asymptote.
Q1) How can I know if this graph is ln(x) or e^x
(I thought it was e^x graph since there's no x-axis intercept , however the answer in marking scheme is:
Domain : xεR , x>-3
Range : yεR
Ast. : x=-3
So it is ln(x) since there is a x-range/value in the domain .(correct me if i am wrong)
Q2) what's the difference between the two following two graphs ,, and how can I find the domain and range ?
Its the Modulus function that confuses me and make it hard to get the domain value.
*No calculations are required from the above question, as it says "from the figure ... "
Thank you,