mikea2424
- 2
- 0
Hello,
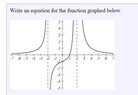
I'm studying for a test this Friday and I have two problems that have completely stumped me. I'm not sure how to solve either. Any help would be greatly appreciated.
View attachment 7234
View attachment 7235
I'm studying for a test this Friday and I have two problems that have completely stumped me. I'm not sure how to solve either. Any help would be greatly appreciated.
View attachment 7234
View attachment 7235