A Intro to String Theory: Lightcone Gauge & Oscillators

[binbagsss]

Lightcone gauge is $X^u=\tau=1/\sqrt{2}(X^0+X^{D-1})$ (1)

The mode expansions are:

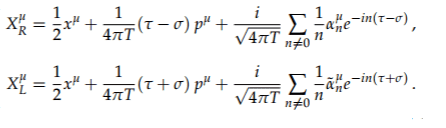
My book says 'it is possible to solve for one of the oscillators in terms of all the others' with this relation.

What is a oscillator? Is this any of the $X^{D}$ coordinates, what exactly does $n$ represent, 'frequencies' of a given oscillator?

Does the notation $X^{D-1}$ refer to any spatial coordinate that is the preferred choice?

So basically the relation (1) reduces the number of equations to solve by one, is this what this statement means?

 

[cosmik debris]

I think X⁰ is the infinite momentum direction i.e. the direction in which the string is travelling. X^D-1 are the dimensions perpendicular to X⁰, the -1 is to remove the time dimension. Each string comprises a number of mass points which are described as harmonic oscillators, n is the number of the oscillator in the string.