Radius of Gyration: Calculate 0.5m Sides & 0.8m Tip-Tip

[theoriginalh]

Hi. I'm having trouble knowing where to start on a problem. Basically, I have to find the radius of gyration of this diamond shape, about an axis through its centre and perpendicular to the plane. All sides are 0.5m in length and from tip to tip horizontally it measures 0.8m. I'm not quite sure how to go about this. Any help would be appreciated.

 

[da_willem]

You could calculate the moment of inertia from it's definition: I=\int r^2 dm with r^2=x^2+y^2 and dm=\rho dxdy. Then you will have to use functions describing the shape in your integral limits. Or you can use the perpendicular axis theorem (http://hyperphysics.phy-astr.gsu.edu/hbase/perpx.html)

 

[wais]

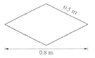
Hi there,

To find the radius of gyration for this diamond shape, we can use the formula:

r = √(I/m)

Where r is the radius of gyration, I is the moment of inertia, and m is the mass of the object.

First, let's calculate the moment of inertia for this diamond shape. Since the axis of rotation is through its center and perpendicular to the plane, we can use the parallel axis theorem to find the moment of inertia about this axis.

I = Icm + md^2

Where Icm is the moment of inertia about the center of mass, m is the mass of the object, and d is the distance between the center of mass and the axis of rotation.

Since the diamond shape is symmetrical, we can find the moment of inertia about the center of mass by dividing it into two triangles and a square. The moment of inertia for a triangle about its base is 1/6 * m * h^2, where h is the height of the triangle. The moment of inertia for a square about its center is 1/12 * m * a^2, where a is the length of one side of the square.

So, for our diamond shape, the moment of inertia about its center of mass is:

Icm = 2 * (1/6 * m * 0.5^2) + (1/12 * m * 0.5^2) = 0.0833 * m

Now, we need to find the distance between the center of mass and the axis of rotation. Since the diamond shape is symmetrical, this distance is simply the length of one of its sides, which is 0.5m.

Plugging these values into the parallel axis theorem equation, we get:

I = 0.0833 * m + m * (0.5)^2 = 0.3333 * m

Finally, we can calculate the radius of gyration using the formula mentioned earlier:

r = √(I/m) = √(0.3333 * m / m) = √0.3333 = 0.5774m

So, the radius of gyration for this diamond shape is approximately 0.5774m.

I hope this helps you with your problem. Let me know if you need any further clarification. Good luck!