Ratio of effective and average voltage

[crom1]

Homework Statement

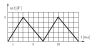
See the diagram. Find $$\frac{U_{ef}}{U_{avg}}$$ .

Homework Equations

[/B]
$$ U_{ef}=\frac{U_m}{\sqrt3} , U_{avg} = \frac{U_m}{2} $$

The Attempt at a Solution

This one should be easy.I know that official solution probably divided $$\frac{2}{\sqrt3} \approx 1.154$$ (which is correct), but I am not sure why can we do that in this case, when we have 2 different kinds of lines, one with
u=5/3 t and second one u=-5/4t+35/4 . What did was found the effective of the first one and the second one, average of first one and second one , used $$ U_{avg}= U_{avg1}+U_{avg2}$$ , and $$U_{ef}^2 = U_{ef1}^2+U_{ef2}^2$$. My question is why is mine incorrect, and the solution shown above correct?

 

[crom1]

Nevermind, I found my mistake, I forgot to multiply with 3/7 and 4/7 and with sqrt(3/7) and sqrt(4/7).