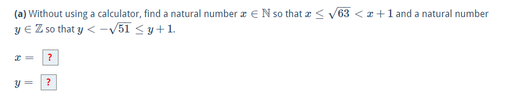danielw
- 5
- 0
Hi All
This is my question.
View attachment 5871
I don't know how to begin working on it.
I already tried simplifying the first part to: $$ \sqrt{63} = \sqrt{7 \cdot 3^3}=\sqrt{7}\sqrt{3^2}=3\sqrt{7}$$
But this doesn't get me closer to answering the first part of the question, and I think the same technique will apply to the second part. I would be grateful for some guidance!
Thanks.
Daniel
This is my question.
View attachment 5871
I don't know how to begin working on it.
I already tried simplifying the first part to: $$ \sqrt{63} = \sqrt{7 \cdot 3^3}=\sqrt{7}\sqrt{3^2}=3\sqrt{7}$$
But this doesn't get me closer to answering the first part of the question, and I think the same technique will apply to the second part. I would be grateful for some guidance!
Thanks.
Daniel