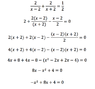Natasha1
- 494
- 9
1. Rearrange the following equation
2/(x-2) + 2/(x+2) = 1/2
into the form Ax2+ Bx + C = 0
I did it and got -x2 + 8x + 4 = 0
Am I correct please?
2/(x-2) + 2/(x+2) = 1/2
into the form Ax2+ Bx + C = 0
I did it and got -x2 + 8x + 4 = 0
Am I correct please?