NovicePWizzard
- 8
- 1
So, on a recent maths paper I sat, there was a question where we had to make t the subject. (Disclaimer, this is not homework. I am simply curious, and cannot see how it works. Please don't Ban me) I could not do it for the life of me, because, seemingly the two ts cancel? I know this shouldn't happen, and my teacher went through it, however I've tried it every which way, and the solution still eludes me.
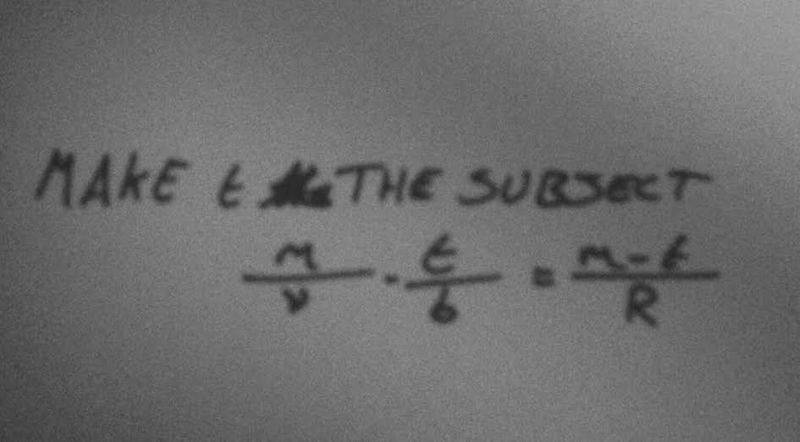
So I tried the following working, which my teacher suggested:

So, I began by combining the fraction on the left, then I cross multiplied, collected all terms with t and... What? I can't seem to get any further, without cancelling, let alone getting rid of the b and R.
Am I seriously missing a trick here? I've never really been that good with algebraic fractions.
Also, any tips on the matter would be well received.
So I tried the following working, which my teacher suggested:
So, I began by combining the fraction on the left, then I cross multiplied, collected all terms with t and... What? I can't seem to get any further, without cancelling, let alone getting rid of the b and R.
Am I seriously missing a trick here? I've never really been that good with algebraic fractions.
Also, any tips on the matter would be well received.