Refraction in a Glass Cylinder with just 1 Number

[Phoenixtears]

Homework Statement

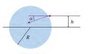
The figure shows a light ray incident on a glass cylinder where h = R/9. At what angle α will the ray be refracted?

(Image Attached)

Homework Equations

n(sin(theta))= N(sin(THETA))

The Attempt at a Solution

I'm not sure how to attack this problem. I've thought of using Snell's law:

1 sin (90) = 1.52 sin (THETA)

But I stopped myself mid-equation because then the R/9 is useless. I have decided to make R= 1 and then h= 1/9 (just to make things simple. I drew the picture and then extended out the refracted arrow, trying to figure out a way to use geometry, but I just can't place it.

Can anyone help me out?

Thanks in advance!

~Phoenix

 

[jambaugh]

The attachment is pending approval so I can't see your picture yet. But you will need Snell's law since the refraction will depend on the materials index. Are there any other parameters? Can you describe were on the cylinder the light is striking? End or round side? Aimed through the axis or offset by some distance?

Remember Snell's law applies to angles relative to the normal of the surface. You have a 90deg in your formula which indicates the light is tangent to the surface. If the light strikes perpendicular to the surface you will have no refraction and angle = 0. If tangent to the surface it doesn't even cross the surface.

 

[Redbelly98]

Hint: what angle does the normal make, with respect to horizontal?

 

[jambaugh]

Hint: what angle does the normal make, with respect to horizontal?

Then normal is perpendicular to the surface. In the case of the cylinder it will be in the direction of a line through the axis of the cylinder and the point where the light hits the surface. You'll find that the radius and the height h above the center form sides of a right triangle. You can use trig to express the angle.