Cole A.
- 12
- 0
(I'd like to preface this with the warning that the following question may be a very dumb one.)
My understanding is that current density (or flux) \vec{J} = \vec{J}(x, y, z) is the rate of flow of charge (or the current) per unit area. (Units of \frac{\text{C/s}}{\text{cm}^2}.)
Say we know that in an irregularly shaped volume conductor (e.g. a nerve fiber, where the irregularity is due to some sort of biological obstruction), the current density \vec{J} has the form given in Figure 1 (see attachments).
The current I is --- I think --- given from Ohm's law: specifically, if the potential difference across the ends of the fiber and the total resistance of the fiber are known, then
<br /> \begin{equation*}<br /> I = \frac{V}{R},<br /> \end{equation*}<br />
which is a scalar quantity. I believe this value is constant for each point (x, y, z) in the fiber, assuming no build-up of current anywhere (by the law of conservation of charge).
Now I know that the surface integral of a flux gives a flow rate, so the surface integral of \vec{J} should give a current. But is the current equal to I? I mean, does
<br /> \begin{equation*}<br /> \iint_S \vec{J} \cdot \vec{n} dS = I<br /> \end{equation*}<br />
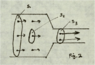
for every S, or only for S = cross-sectional area of the conductor? The reason I ask is because, if I draw three example surfaces S_1, S_2, S_3 (Figure 2), the surface integral of \vec{J} over S_1 is obviously not equal to that over S_2.
So I guess what I am asking is: is
<br /> \begin{equation*}<br /> I = \iint_{S_1} \vec{J} \cdot \vec{n} dS_1 = \iint_{S_3} \vec{J} \cdot \vec{n} dS_3 \neq \iint_{S_2} \vec{J} \cdot \vec{n} dS_2<br /> \end{equation*}<br />
true, where I is current as found from Ohm's law? And if so, does this mean that any current I through a conductor is not simply the rate of flow of charge, but a rate of flow of charge implicitly with respect to the cross-sectional area?
Thanks
My understanding is that current density (or flux) \vec{J} = \vec{J}(x, y, z) is the rate of flow of charge (or the current) per unit area. (Units of \frac{\text{C/s}}{\text{cm}^2}.)
Say we know that in an irregularly shaped volume conductor (e.g. a nerve fiber, where the irregularity is due to some sort of biological obstruction), the current density \vec{J} has the form given in Figure 1 (see attachments).
The current I is --- I think --- given from Ohm's law: specifically, if the potential difference across the ends of the fiber and the total resistance of the fiber are known, then
<br /> \begin{equation*}<br /> I = \frac{V}{R},<br /> \end{equation*}<br />
which is a scalar quantity. I believe this value is constant for each point (x, y, z) in the fiber, assuming no build-up of current anywhere (by the law of conservation of charge).
Now I know that the surface integral of a flux gives a flow rate, so the surface integral of \vec{J} should give a current. But is the current equal to I? I mean, does
<br /> \begin{equation*}<br /> \iint_S \vec{J} \cdot \vec{n} dS = I<br /> \end{equation*}<br />
for every S, or only for S = cross-sectional area of the conductor? The reason I ask is because, if I draw three example surfaces S_1, S_2, S_3 (Figure 2), the surface integral of \vec{J} over S_1 is obviously not equal to that over S_2.
So I guess what I am asking is: is
<br /> \begin{equation*}<br /> I = \iint_{S_1} \vec{J} \cdot \vec{n} dS_1 = \iint_{S_3} \vec{J} \cdot \vec{n} dS_3 \neq \iint_{S_2} \vec{J} \cdot \vec{n} dS_2<br /> \end{equation*}<br />
true, where I is current as found from Ohm's law? And if so, does this mean that any current I through a conductor is not simply the rate of flow of charge, but a rate of flow of charge implicitly with respect to the cross-sectional area?
Thanks