Luis Babboni
Hi people!
First of all, sorry for my poor english.
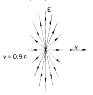
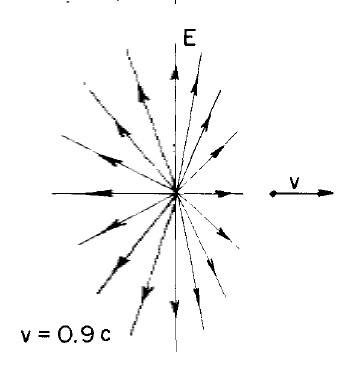
I read in many places and I did the calculus and I agree that the field of a moving charge have this aspect:
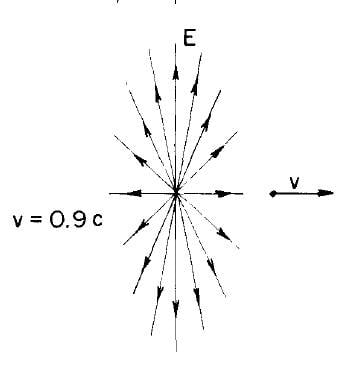
(Taked from Feynman´s Lectures on Physics chapter 26th.)
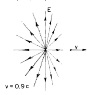
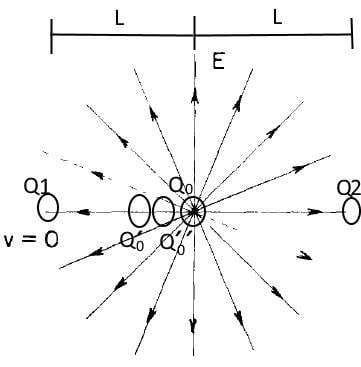
But my problem is in that my intuition says me that it must be something like this:
I´m talking just about intensity in the same direcction of v, I still not work with perpendicular to v intensity.
My reasoning to say that is the following:
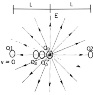
When in an innertial system where Q1 and Q2 are at rest both at distance L of to Q0 that is moving to right, cause Q2 "sees" the field produced by Q0 when Q0 was at, say, Q0´ and Q1 "sees" the field produced by Q0 when Q0 was at, say, Q0´´. And cause distance Q1-Q0´´ is smaller than distance Q1-Q0 and distance Q2-Q0´ is greater than distance Q2-Q0, the intensity of the field at Q2 must be smaller than intensity of the field if Q0 is at rest in the same system than Q1 and Q2 (that are the field you see in the next picture) and the intensity of the field at Q1 must be greater than the field if Q0 is at rest in the same system than Q1 and Q2. Ant then you could see something like I draw in the second picture.
Cause I always talk about an inertial system where Q1 and Q2 are at rest and L is a proper distance in it, I do not see the necesity of any Lorentz transformation...
Of course I´m wrong! :-D
But could someone explain me where is my mistake?
Thanks!
First of all, sorry for my poor english.
I read in many places and I did the calculus and I agree that the field of a moving charge have this aspect:
(Taked from Feynman´s Lectures on Physics chapter 26th.)
But my problem is in that my intuition says me that it must be something like this:
I´m talking just about intensity in the same direcction of v, I still not work with perpendicular to v intensity.
My reasoning to say that is the following:
When in an innertial system where Q1 and Q2 are at rest both at distance L of to Q0 that is moving to right, cause Q2 "sees" the field produced by Q0 when Q0 was at, say, Q0´ and Q1 "sees" the field produced by Q0 when Q0 was at, say, Q0´´. And cause distance Q1-Q0´´ is smaller than distance Q1-Q0 and distance Q2-Q0´ is greater than distance Q2-Q0, the intensity of the field at Q2 must be smaller than intensity of the field if Q0 is at rest in the same system than Q1 and Q2 (that are the field you see in the next picture) and the intensity of the field at Q1 must be greater than the field if Q0 is at rest in the same system than Q1 and Q2. Ant then you could see something like I draw in the second picture.
Cause I always talk about an inertial system where Q1 and Q2 are at rest and L is a proper distance in it, I do not see the necesity of any Lorentz transformation...
Of course I´m wrong! :-D
But could someone explain me where is my mistake?
Thanks!