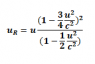scottJH
- 6
- 0
Homework Statement
In a given inertial frame two particles are shot out simultaneously from a given point with equal speeds u at an angle of 60 degrees with respect to each other. Using the concept of 4-velocity or otherwise, show that the relative speed of the particles is given by
##u_R = u(1-3u^2/4c^2)/(1-u^2/2c^2)##
I have tried this a number of ways but always end up getting
##u_R = u(1-3u^2/4c^2)##
So I guess my question is which answer is correct?
Homework Equations
##u'_x = (ux-v)/(1-v*ux/c^2)## and ##u'_y = uy/\gamma(1-v*ux/c^2)##
The Attempt at a Solution
[/B]
I set S' as the stationary state of particle A, moving at a velocity u in the x direction. This meant that particle A was at rest in this frame. Therefore the velocity of B in the S' frame is the relative velocity of the two particles.
For particle B I obtained:
##u'_x = -u/2## and ##u'_y = usin60/\gamma##
Then using those values calculated the relative velocity to be
##u_R = u(1-3u^2/4c^2)##I apologise for the layout of the equations because it is my first time posting.
Attachments
Last edited: