Learn Relativity Using the Bondi K-calculus
Although Special Relativity was formulated by Einstein (1905), and given a spacetime interpretation by Minkowski (1908) [which helped make special relativity more accessible and acceptable], it could be argued that these approaches are still too abstract and too mathematical for most students.
In the early 1960s, Hermann Bondi advocated a presentation of special relativity (called the k-calculus [which involves no calculus–just simple algebra]) that is advertised to be a “simple logical extension of well-known Newtonian ideas, without any of its mathematical trappings.” (I think what this means is that Bondi will de-emphasize and postpone the derivation of the Lorentz Transformation.)
This approach is presented in his book “Relativity and Common Sense” (1962, 1964). In addition, Bondi presented “E=mc2: Thinking Relativity Through”, a series of ten lectures on BBC TV running from Oct 5 to Dec 7, 1963. [Are these accessible online?] There is an accompanying pamphlet “E=mc2: An Introduction to Relativity” (www.worldcat.org/title/emc2-an-introduction-to-relativity/oclc/156217827) .
Unfortunately, Bondi’s simple approach is not well-known.
I haven’t seen it in any introductory physics or modern physics textbook. Physics majors might encounter it in intermediate-level introductions to relativity (e.g. Woodhouse, d’Inverno, Ellis&Williams, which–may be not surprising–are authored by relativists who studied at British universities). My earlier Insight ( Relativity on Rotated Graph Paper ) is, in part, my attempt to replace some of the algebra of the k-calculus by counting and arithmetic.
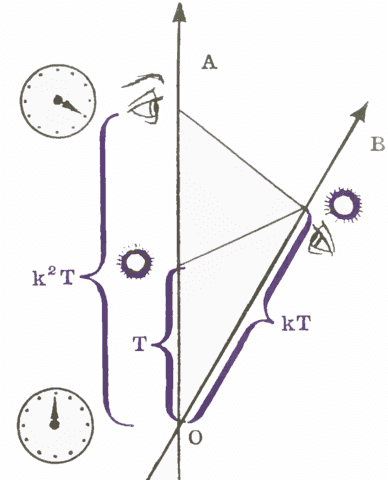
The radar-diagram from Bondi’s pamphlet [corrected version].
(When my audience is students in an introductory course, I would simplify the presentation given below.)
[Admittedly, if you want a quick presentation, the Wikipedia entry is pretty good https://en.wikipedia.org/wiki/Bondi_k-calculus .]
To explain Bondi’s diagram above, let me first describe a more general situation, with a little extra notation [for clarity].
Table of Contents
the k-factor
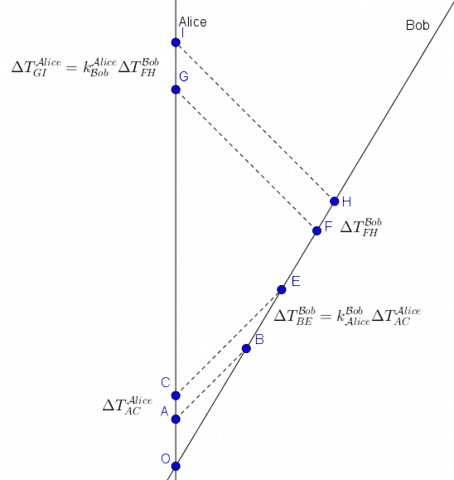
In the above diagram, OA and OB are along the worldlines of inertial observers, Alice and Bob, who met momentarily at event O. Henceforth, we assume that the speed of light is the same for all inertial observers… and we have chosen units so that all light-signals are drawn at 45-degrees.
Later, Alice broadcasts a 1-hour TV show starting at event A and ending at event C on her worldline–thus, ##\Delta T_{AC}^{\cal Alice}=1## hour. Due to the finite speed of light, there is a delay before Bob starts receiving the broadcast. Bob receives the transmitted show starting at event B and ending at event E on his worldline. Since, after event O, Bob and Alice are steadily separating, it takes longer for the transmission at event C to arrive at event E, compared to the transmission at event A to arrive at event B. In other words, it takes longer than 1 hour for Bob to view Alice’s 1-hour show–Bob views Alice’s 1-hour show in slow motion.
Call this slow-down factor for Bob watching Alice ##k^{\cal Bob}_{\cal Alice}##. If Bob, at some distance away, were at rest with respect to Alice, there would still be a delay for Bob, but the slow-down factor ##k^{\cal Bob}_{\cal Alice}## would be equal to 1 [no slow down]. The greater the rate of separation, the larger the slow-down factor. This factor does not depend on when Alice began broadcasting after event O or how long her broadcast lasted. This factor depends only on the relative speed between Alice and Bob. That is, ##k^{\cal Bob}_{\cal Alice}## is a proportionality constant. (Mathematically, think “scaling”… or “similar triangles”. Physically, think “ratio of the period of reception by the receiver to the period of transmission of the source”… “Doppler factor”.)
Analogously, when Bob broadcasts a show to Alice, she views it in slow motion with slow-down factor ##k^{\cal Alice}_{\cal Bob}##. By the Principle of Relativity, these factors must be equal. So, let us refer to these factors as simply ##k## (and henceforth refer to it as the ##k##-factor relating to these observers).
So, how does one measure k?
Radar Diagram for k2
If we knew the period between the tickmarks of Bob’s wristwatch along Bob’s worldline, we could determine ##k##. Either we ask Bob how long it took to watch Alice’s 1-hour show, or we ask Bob to broadcast a 1-hour show and ask Alice how long it took for her to watch it. However, often the situation is that we don’t know the period between Bob’s ticks–one has to calibrate Bob’s wristwatch.
We demonstrate a radar method that Alice can use, which uses her wristwatch and radar signals she sends to and receives from Bob. Alice broadcasts her 1-hour show to Bob, who immediately rebroadcasts [or passively reflects] it back to Alice. So, Alice watches her originally broadcasted 1-hour show in super-slow-motion… with factor ##k^2##.
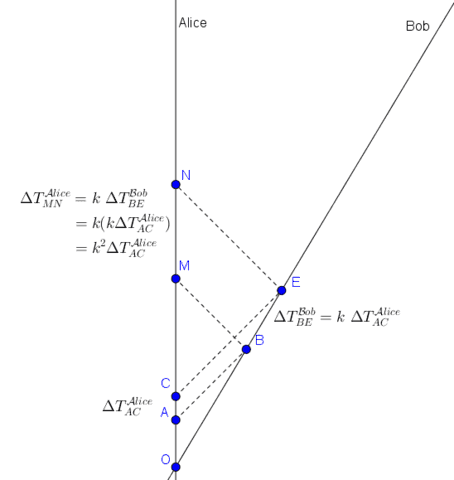
So, the ratio of reflected-reception period to transmission period is ##{\displaystyle\frac{\Delta T^{\cal Alice}_{MN}}{\Delta T^{\cal Alice}_{AC}}}={\displaystyle\frac{k^2\Delta T^{\cal Alice}_{AC}}{\Delta T^{\cal Alice}_{AC}}}=k^2##, which is independent of ##\Delta T^{\cal Alice}_{AC}## and event ##A##. (Note the similarity of ##\bigtriangleup ABM## and ##\bigtriangleup CEN##.)
Now, let’s simplify Bondi’s diagram by starting the broadcast at event O and ending at event C [effectively moving events A, B, and M to coincide with event O].
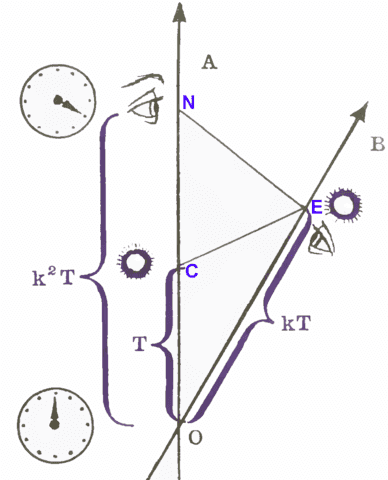
Interpreting k and Calculating with k
To interpret ##k## in more familiar terms, Alice measures vector ##\vec {OE}## using a radar method to assign (t,x)-coordinates to distant event E on Bob’s worldline. [The set of radar events (##C## and ##N##) for Alice to measure event E is determined by the intersection of Alice’s inertial worldline and the light-cone of event E. Alice chooses an origin event ##O## on her worldline, which is often the separation event for convenience.]
We provide the calculations here. (For details, consult https://en.wikipedia.org/wiki/Bondi_k-calculus#Radar_measurements_and_velocity or my Insight Relativity on Rotated Graph Paper )
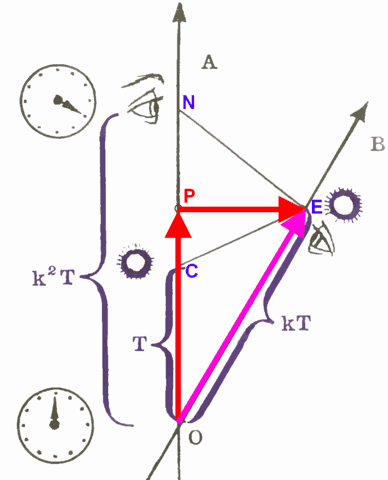
Alice assigns an elapsed time ##\Delta t_{OE}## as average of her radar times (half the sum of) ##\Delta t_{ON}## and ##\Delta t_{OC}.##
(This defines an event P on Alice’s worldline that Alice regards as simultaneous with distant event E. That is, for Alice, ##\Delta t_{OP}=\Delta t_{OE}##. Geometrically, P is the midpoint of segment CN—although this wasn’t drawn accurately in Bondi’s diagram.)
$$\Delta t_{OE}=\frac{1}{2}(k^2T + T)$$
The spatial distance ##\Delta x_{OE}## is half of the round-trip time (half the difference), times the speed of light ##c##,
$$\Delta x_{OE}=\frac{1}{2}c(k^2T – T)$$
(For Alice, this means that ##\Delta x_{OE}=\Delta x_{PE}## and thus, ##\vec {OE}=\vec {OP}+\vec {PE}##,
where ##\vec {OP}## and ##\vec {PE}## are along Alice’s time- and space-axes [and are thus Minkowski-perpendicular]. )
The [constant] velocity is therefore
$$V_{OE}=\frac{\Delta x_{OE}}{\Delta t_{OE}}=\frac{\frac{1}{2}c(k^2T – T)}{\frac{1}{2}(k^2T + T)}=\frac{k^2-1}{k^2+1}c$$
Rather than solve the above velocity equation for ##k##, let us add and subtract the expressions for elapsed time and spatial distance to get ##k##:
$$\Delta t+\frac{\Delta x}{c}=k^2 T$$
$$\Delta t-\frac{\Delta x}{c}=T,$$
which expresses the radar times on Alice’s worldline to measure ##\vec {OE}##, in terms of the elapsed time and spatial distance (that is, the time- and space-components of ##\vec {OE}## according to Alice).
These are related to “light-cone coordinates“, the coordinates in the eigenbasis of the Lorentz Transformation. In my convention, ##\Delta u=\Delta t+\frac{\Delta x}{c}## and ##\Delta v=\Delta t-\frac{\Delta x}{c}##. So, these equations be rewritten as
$$\Delta u=k^2 T$$
$$\Delta v=T,$$
The ##k##-factor is an eigenvalue of the Lorentz Transformation. [See my earlier insight for details: Relativity Variables: Velocity, Doppler-Bondi k, and Rapidity.]
- By division [or by eliminating ##T##],
$$k^2 =\frac{\Delta u}{\Delta v}=\frac{\Delta t+\frac{\Delta x}{c}}{\Delta t-\frac{\Delta x}{c}}=\frac{1+\frac{\Delta x}{c\Delta t}}{1-\frac{\Delta x}{c\Delta t}}=\frac{1+(V/c)}{1-(V/c)},$$we recognize that the ##k##-factor is the Doppler factor $$k=\sqrt{\frac{1+(V/c)}{1-(V/c)}}.$$ - By multiplication, we obtain an interesting expression of the square-magnitude of ##\vec {OE}## [on Bob’s worldline] in terms of a Pythagorean-like combination involving ##k## and Alice’s ##\Delta t## and ##(\Delta x/c)## and her ##T## (which we have made explicit):
$${\Delta u}{\Delta v}=\left(\Delta t^{\cal Alice}_{OE}\right)^2-\left(\frac{\Delta x^{\cal Alice}_{OE}}{c}\right)^2=(k_{Alice,Bob} T^{\cal Alice})^2,$$
Using ##\Delta t^{\cal Bob}_{OE}=k_{Alice,Bob} T^{\cal Alice}##, we have
$${\Delta u}{\Delta v}=\left(\Delta t^{\cal Alice}_{OE}\right)^2-\left(\frac{\Delta x^{\cal Alice}_{OE}}{c}\right)^2=(\Delta t^{\cal Bob}_{OE})^2,$$
where the expression on the right depends on Bob’s measurements alone [not Alice’s].
This suggests that if another observer, (say) Carol, measures ##\vec {OE}##, her components would satisfy an expression of the same form. That is,
$${\Delta u^{\cal Carol}}{\Delta v^{\cal Carol}}=\left(\Delta t^{\cal Carol}_{OE}\right)^2-\left(\frac{\Delta x^{\cal Carol}_{OE}}{c}\right)^2=(\Delta t^{\cal Bob}_{OE})^2.$$
In other words, for any observer measuring ##\vec{OE}##, the expression ##{\Delta u^{\cal obs}_{OE}}{\Delta v^{\cal obs}_{OE}}## or equivalently ##\left(\Delta t^{\cal obs}_{OE}\right)^2-\left(\frac{\Delta x^{\cal obs}_{OE}}{c}\right)^2## is an invariant, independent of observer. This is called the “squared-interval of ##\vec{OE}##”, denoted by ##\Delta s^2_{OE}##.
- It was observed by N.D Mermin (“Space-time intervals as light rectangles,” N. D. Mermin, Am. J. Phys. 66, 1077–1080 (1998); http://dx.doi.org/10.1119/1.19047 ) that the Doppler factor ##k## and the square-interval ##\Delta s^2_{OE}## describe the aspect-ratio ##\frac{\Delta u}{\Delta v}## and the area ##{\Delta u}{\Delta v}##of the “causal diamond” of OE. This was the inspiration of my AJP article (“Relativity on rotated graph paper,” Roberto B. Salgado, Am. J. Phys. 84, 344-359 (2016); http://dx.doi.org/10.1119/1.4943251 ). See also my Relativity of Rotated Graph Paper Insight for details.
Formulas for Velocity Composition and the Lorentz Transformation
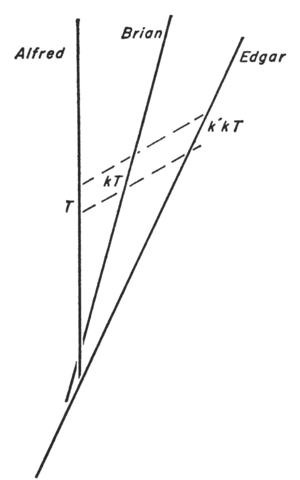
Bondi, in his Relativity and Common Sense (archive.org/details/RelativityCommonSense), derives the Velocity Composition and Lorentz Transformation formulas. We’ll switch to Bondi’s names: Alfred, Brian, and Edgar.
velocity composition
From Bondi’s diagram above, if Alfred broadcasts a ##T=1##-hour show, Brian watches that in ##k^{\cal Brian}_{\cal Alfred}T## hours (called ##kT## in the diagram). If Edgar watches Brian’s instant rebroadcast, it takes Edgar ##k^{\cal Edgar}_{\cal Brian}(k^{\cal Brian}_{\cal Alfred} T) ## hours (called ##k’kT## in the diagram), which could be thought of as Edgar watching Alfred’s original ##T=1##-hour show in ##k^{\cal Edgar}_{\cal Alfred}T## hours. Thus, ##k^{\cal Edgar}_{\cal Alfred}T=k^{\cal Edgar}_{\cal Brian}(k^{\cal Brian}_{\cal Alfred} T)##, which implies this multiplicative relation of k-factors
$$k^{\cal Edgar}_{\cal Alfred}=k^{\cal Edgar}_{\cal Brian}k^{\cal Brian}_{\cal Alfred}.$$
Since ##\displaystyle V^{\cal Edgar}_{\cal Alfred}=\frac{(k^{\cal Edgar}_{\cal Alfred})^2-1}{(k^{\cal Edgar}_{\cal Alfred})^2+1}c=\frac{(k^{\cal Edgar}_{\cal Brian} k^{\cal Brian}_{\cal Alfred})^2-1}{(k^{\cal Edgar}_{\cal Brian}k^{\cal Brian}_{\cal Alfred})^2+1}c##
and
##\displaystyle (k^{\cal Edgar}_{\cal Brian})^2={\frac{1+V^{\cal Edgar}_{\cal Brian}/c}{1-V^{\cal Edgar}_{\cal Brian}/c}}## and ##\displaystyle (k^{\cal Brian}_{\cal Alfred})^2={\frac{1+V^{\cal Brian}_{\cal Alfred}/c}{1-V^{\cal Brian}_{\cal Alfred}/c}}##,
we obtain
$$V^{\cal Edgar}_{\cal Alfred}=\frac{V^{\cal Edgar}_{\cal Brian}+V^{\cal Brian}_{\cal Alfred}}{1+V^{\cal Edgar}_{\cal Brian}V^{\cal Brian}_{\cal Alfred}/c^2}.$$
(Sorry, if it looks cluttered… but, in this case, I think it’s better than ‘, ”, and unprimed. In a calculation by hand, I used initials instead of full names.)
Lorentz Transformation
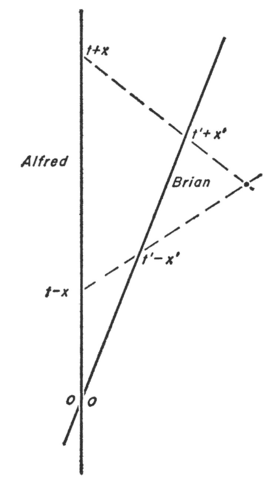
From Bondi’s diagram above, we have two inertial observers doing a radar experiment to assign coordinates to a distant event. Note the intersections of their worldlines with the lightcone of the distant event. Bondi has absorbed the factor of ##c## into the units of distance.
Restoring the factors of ##c##, we have in rectangular and light-cone coordinates:
$$(t+\frac{x}{c})=k(t’+\frac{x’}{c})\qquad u=ku’$$
$$(t’-\frac{x’}{c})=k(t-\frac{x}{c})\qquad v’=kv$$
Putting the primed quantities (Brian’s measurements) on the left, we have
$$(t’+\frac{x’}{c})=\frac{1}{k}(t+\frac{x}{c})\qquad u’=\frac{1}{k}u$$
$$(t’-\frac{x’}{c})=k(t-\frac{x}{c})\qquad v’=kv$$
By multiplication, the ##k##-factors cancel to display the invariance of the square-interval
$$t’^2-\left(\frac{x’}{c}\right)^2=t^2-\left(\frac{x}{c}\right)^2\qquad u’v’=uv.$$
By addition and subtraction, we can solve the system of equations for ##t’## and ##x’##:
##
\begin{align*}
(t’+\frac{x’}{c})+(t’-\frac{x’}{c})
&=\frac{1}{k}(t+\frac{x}{c})+k(t-\frac{x}{c})\\
2t’&=(k^{-1}+k)t+(k^{-1}-k)\frac{x}{c}\\
t’&=\left(\frac{k+k^{-1}}{2}\right)t-\left(\frac{k-k^{-1}}{2}\right)\frac{x}{c}=(\gamma) t – (\gamma V) \frac{x}{c}
\end{align*}
##
##
\begin{align*}
(t’+\frac{x’}{c}) – (t’-\frac{x’}{c})
&=\frac{1}{k}(t+\frac{x}{c}) – k(t-\frac{x}{c})\\
2\frac{x’}{c}&=(k^{-1} – k)t+(k^{-1} + k)\frac{x}{c}\\
\frac{x’}{c}&= -\left(\frac{k – k^{-1}}{2}\right)t +\left(\frac{k + k^{-1}}{2}\right)\frac{x}{c}= -(\gamma V) t +(\gamma) \frac{x}{c}
\end{align*}
##
where ##k=\sqrt{\frac{1+\frac{V}{c}}{1-\frac{V}{c}}}## and ##\gamma=\frac{1}{\sqrt{1-\left(\frac{V}{c}\right)^2}}##.
These relationships between ##k##, ##V##, and ##\gamma## are possibly less obscure when one recognizes that ##k=e^\theta##, ##V=c\tanh\theta##, and ##\gamma=\frac{e^\theta+e^{-\theta}}{2}=\cosh\theta##, where ##\theta## is the rapidity[-angle]. [See my earlier insight for details: Relativity Variables: Velocity, Doppler-Bondi k, and Rapidity.]
So, in Bondi’s method, special relativity [in (1+1)-dimensions] can be developed, with physical interpretation and relatively simple arithmetic, from ##k## (the Doppler factor). Note that the square roots may appear at the end of a calculation if one wishes to express things in terms of ##V## instead of ##k##.
Further Reading
“Relativity and Common Sense” Hermann Bondi (Dover, 1962);
available at archive.org/details/RelativityCommonSense .
“E=mc2: Thinking Relativity Through”, a series of ten lectures by Hermann Bondi on BBC TV running from Oct 5 to Dec 7, 1963. [Are these accessible online?]
http://genome.ch.bbc.co.uk/schedules/bbctv/1963-10-05
“E=mc2: An Introduction to Relativity”, Hermann Bondi
[a pamphlet that accompanies the BBC broadcast]
(www.worldcat.org/title/emc2-an-introduction-to-relativity/oclc/156217827) .
https://en.wikipedia.org/wiki/Bondi_k-calculus
“Space-time intervals as light rectangles,” N. D. Mermin,
Am. J. Phys. 66, 1077–1080 (1998); http://dx.doi.org/10.1119/1.19047
“Relativity on rotated graph paper,” Roberto B. Salgado,
Am. J. Phys. 84, 344-359 (2016); http://dx.doi.org/10.1119/1.4943251
[see also the references within]
my related Insights:
https://www.physicsforums.com/insights/relativity-variables-velocity-doppler-bondi-k-rapidity/
https://www.physicsforums.com/insights/relativity-rotated-graph-paper/
Professor of Physics (BS,MS,PhD), Math (BS). Interested in relativity, physics, mathematics, computation, physics pedagogy.






There is a circularity in the idea of measuring the speed of light: to measure the speed you need synchronized clocks; but you can't get distant clocks synchronized unless you know the speed of light.The one-way speed of light, yes. That's why it's the two-way speed that is considered invariant. The one-way speed is conventionally assumed to be equal to the two-way speed, but there's no way to test this.
The only way out of it, says Einstein, is to assume (stipulate) that the time it takes light to go from A to B = the time it takes to go from B to A.A way out of it. I derived some of the maths for inertial frames assuming otherwise here. It's not difficult, just ugly.
Some scientists and philosophers take the "1/2" to be a variable, as if it were an arbitrary choice among a range of other possible values, making the definition into a convention. But there are no other possible, ie. empirically determinable, values,Not quite; there are no empirically determinable values for the one way speed of light – that's why it's a convention. Choosing another value is simply choosing a different coordinate system in spacetime. Most people don't do it for inertial frames because it's ugly, unintuitive, makes the maths more complex, and adds nothing over the simple symmetric assumption – but there is nothing preventing it.
and because it is a one clock measurement of a round-trip, the constancy of the speed of the sigal follows as a logical inference.Why do you think that this doesn't apply to one clock measurements of the round-trip speed of a ball? Or a sound wave? What's special about light that there is a "logical identity" with its behaviour but nothing else?
There is a circularity in the idea of measuring the speed of light: to measure the speed you need synchronized clocks; but you can't get distant clocks synchronized unless you know the speed of light. It's a logical circle.My desk has a width of 0.500 000 000 m. I shall send a pulse of light from one end to the other and have it reflect back to arrive at the source. The time it took was ##frac{1}{299 792 458}## seconds. I therefore measure the speed of light to be 299 792 458 m/s.
There was nothing circular in the logic, and there was no synchronization of clocks. I used only one clock!
There is a circularity in the idea of measuring the speed of light: to measure the speed you need synchronized clocks; but you can't get distant clocks synchronized unless you know the speed of light. It's a logical circle. The only way out of it, says Einstein, is to assume (stipulate) that the time it takes light to go from A to B = the time it takes to go from B to A. Now that is how Einstein originally put it, and it makes it sound like an assumption and a matter of convention, which happily, fortuitously, agrees with the actual behavior of light signals. That is not the right way to put it: the language is old fashioned and betrays the thought, which is that the only way to synchronize distant clocks, A and B, is the one-clock method of sending a signal from A to B and back again and taking half of the interval of time and adding it to the start time at A to get the time at B (in accordance with the definition). Some scientists and philosophers take the "1/2" to be a variable, as if it were an arbitrary choice among a range of other possible values, making the definition into a convention. But there are no other possible, ie. empirically determinable, values, because of the logical conundrum above. If there are other way–slow transport is rubbish–they will be logically equivalent to Einstein's, if they are valid, because E. has the concept of simultaneity down pat. It is reflexive, symmetrical, and transitive–the logical form of identity of time–and because it is a one clock measurement of a round-trip, the constancy of the speed of the sigal follows as a logical inference. That's why E. was not surprised at all by the non-outcome of Michelson-Morely.
It is a bit of logic that has to do with the only possible way of synchronizing (distant) clocks and measuring time.Taking advantage of the fact that the speed of light is invariant is not the only way to synchronize spatially separated clocks. And it's not necessary for measuring time. Time is a physical quantity. Synchronization of spatially separated clocks is a convention. There are many ways to do it. Some are equivalent and some aren't.
So he made the assumption
This puts it in the wrong light. Einstein was quite explicit: the constancy of the speed of light is not an assumption (an hypothesis or an empirical generalization). It is a bit of logic that has to do with the only possible way of synchronizing (distant) clocks and measuring time. It is a conceptual necessity, not a fact about the nature of light.I'm not quite sure what you mean by this. In his 1905 paper Einstein calls the constancy of the speed of light a "principle", although it's more often referred to as a "postulate". Either way, it's something he assumed. It's the basis of his reasoning, yes, and it isn't necessary for light to travel at the invariant speed for there to be an invariant speed. But neither fact makes Einstein's postulates anything other than postulates.
About forty years before Einstein, Maxwell published equations describing electromagnetism. One solution to the equations was a wave, which turned out to have the properties of light. One weird thing was that the speed of the wave came out the same always. Naturally everyone assumed that the equations weren't quite right and the hunt was on to find the problem.
The next forty years were a bit confusing as no one could find anthing wrong. Experiments that were expected to help (e.g. Michelson and Morley) didn't work as predicted, but did provide some ad hoc patches. Einstein had the insight that if the (apparently daft) prediction that light always travels at the same speed for all inertial observers was correct then he could explain all of the confusion. So he made the assumption.So he made the assumption
This puts it in the wrong light. Einstein was quite explicit: the constancy of the speed of light is not an assumption (an hypothesis or an empirical generalization). It is a bit of logic that has to do with the only possible way of synchronizing (distant) clocks and measuring time. It is a conceptual necessity, not a fact about the nature of light.
The theory of special relativity was derived from a simple fact based on the right triangle as follows :
Imagine a light signal is sent from a point to an observer moving with a velocity "v". This signal will be received by this observer moving with velocity "v" after a time delay with respect to the initial position of this observer that forms the hypotenus of the right triangle on which the velocity of light "c" is the same as the one of the right sides of the right triangle while for the other right side the velocity of the observer is "v". If you multiply these velocities with the same time difference "dt", addition of squares of the two right sides would be greater than the square of the hypotenus that would violate the pytogoran theorem for which it becomes necessary to denominate the time intervals with different indices as : :
(cdt*)^2 = (vdt*)^2 + (cdt)^2 which after a simple algebra becomes dt* = dt / [ 1 – (v/c)^2 ]^1/2
Alice's movie is seen by Bob to be in slow motion, and Bob's movie is seen by Alice to be in slow motion. That is similar to SR in which Alice's and Bob's clocks would measure to each other to run slow … but all your diagrams are presenting the case of increasing separation of the inertial travelers.
To the degree that the diagram tends to suggest that movie duration is a proxy for time dilation… it looks like it only works with cases of increasing separation, not cases of approach. Students would notice this…These viewings of movies are not proxies for time-dilation… they are descriptions of the Doppler effect for light.
For observers receding from each other, each observes a "redshift" (or, in the case for sound, a lowering of frequency).
For observers approaching each other, each observes a "blueshift" (or, in the case for sound, a raising of frequency).
In some sense, the Doppler Effect needs the time-dilation factor in order to satisfy the principles of relativity.
Indeed, in the derivation of receding sources and receding receivers,
one gets expressions involving the sound-Doppler factor and the time-dilation factor:
##gamma(1+beta)=left(frac{1}{sqrt{(1-beta)(1+beta)}}right)(1+beta)=sqrt{frac{1+beta}{1-beta}}=k##
and ##frac{1}{gamma}left(frac{1}{1-beta}right)=left(sqrt{(1-beta)(1+beta)}right)left(frac{1}{1-beta}right)=sqrt{frac{1+beta}{1-beta}}=k##.
It might be useful to point out a distinction between time-dilation and the Doppler effect for light.
For two inertial observers Alice and Bob that met at event O,
say "event P on Alice's worldline" and "event Q on Bob's worldline that Alice says is simultaneous with P"
(so, ##vec{PQ}## is a purely-spatial displacement vector according to Alice… it is Minkowski-perpendicular to ##vec{OP}##).
say "event P on Alice's worldline" and "event S on Bob's worldline which is in the lightlike-future of P"
(so, ##vec{PS}## is a future-lightlike displacement vector).
If these movies were youtube videos, there would be a time indicator rolling at the bottom of the screen, so for example, both Alice and Bob could see that Alice's movie indicates that it starts at 00:00:00 and increments to 00:60:00 at the end. Although Bob can't necessarily "view Alice's clock" , he can see by the video time index that in comparison to his own clock her video is running slow… suggesting that her time is slower relative to his (and likewise his to hers when he sends video to her).
When Alice and Bob approach each other, it looks like Bob is going to see Alice's movie running faster (shorter time), and Bob's movie will be seen by Alice to be running faster… so this is not similar to SR which would maintain that each measure each others clocks running slow.In the case of approaching, one has a diagram like this [based on reflecting the original diagram from the Insight]:
View attachment 198701
where I have used a "factor" ##kappa## (kappa).
So, as you said, Bob would view Alice's T-hour broadcast "sped up", in only ##kappa T## hours (where ##kappa<1##).
By similar triangles, ##displaystylefrac{kappa T}{T}=frac{kT}{k^2T}##, which implies that ##kappa=frac{1}{k}##.
Note that since ##k=sqrt{frac{1+beta}{1-beta}}##,
we have ##kappa=frac{1}{k}=sqrt{frac{1-beta}{1+beta}}##, which is the original expression for "##k##" with "velocity ## -beta##".
Thus, there's no need to use ##kappa##… "receding and approaching" are handled by ##k##.
To the degree that the diagram tends to suggest that movie duration is a proxy for time dilation… it looks like it only works with cases of increasing separation, not cases of approach. Students would notice this…That's difference between "see" and "observe". We see Doppler shifted light as it enters our eyes in the same way as we see the movie running slow as its images enter our eyes.
But if you want to observe what is really happening you have to allow for the light travel time. That will lead you to time dilation.
Note that even for the case of increasing separation the time dilation factor is not the same as the Doppler factor.
If the relative speed is ##beta## then the time dilation factor is ##(1-beta^2)^{frac{1}{2}}## whereas the Doppler factor is ##big(frac{1+beta}{1-beta}big)^{pmfrac{1}{2}}##.
Alice's movie is seen by Bob to be in slow motion, and Bob's movie is seen by Alice to be in slow motion. That is similar to SR in which Alice's and Bob's clocks would appear to each other to run slow … but all your diagrams are presenting the case of increasing separation of the inertial travelers.
To the degree that the diagram tends to suggest that movie duration is a proxy for time dilation… it looks like it only works with cases of increasing separation, not cases of approach. Students would notice this…
If these movies were youtube videos, there would be a time indicator rolling at the bottom of the screen, so for example, both Alice and Bob could see that Alice's movie indicates that it starts at 00:00:00 and increments to 00:60:00 at the end. Although Bob can't necessarily "view Alice's clock" , he can see by the video time index that in comparison to his own clock her video is running slow… suggesting that her time is slower relative to his (and likewise his to hers when he sends video to her).
When Alice and Bob approach each other, it looks like Bob is going to see Alice's movie running faster (shorter time), and Bob's movie will be seen by Alice to be running faster… so this is not similar to SR which would maintain that each see each others clocks running slow.
About forty years before Einstein, Maxwell published equations describing electromagnetism. One solution to the equations was a wave, which turned out to have the properties of light. One weird thing was that the speed of the wave came out the same always. Naturally everyone assumed that the equations weren't quite right and the hunt was on to find the problem.
The next forty years were a bit confusing as no one could find anthing wrong. Experiments that were expected to help (e.g. Michelson and Morley) didn't work as predicted, but did provide some ad hoc patches. Einstein had the insight that if the (apparently daft) prediction that light always travels at the same speed for all inertial observers was correct then he could explain all of the confusion. So he did.
Why does he assume the velocity of light is the same for all inertial observers?
Thanks. I was torn between making it as elementary as possible for a beginner (which would only be a tweak on Bondi or just the equations already provided by Wikipedia) or making clarifications and connections to geometry (the logical next step).
Thanks for posting this. A lot of times I want to refer people to Bondi's approach, as I also feel it's one of the best elementary treatments for the person new to relativity. I can and do refer interested people to his book, but it's nice to have a more accessible source.
Yeah like anyone would click those links.
Preface to <<The Theory of Nature’s Mystery>> – The Paradox of the Basic Unit of the Universe
The basic unit of the universe, it is the composition material of any natural existence, the atoms, molecules, electrons, ions, photons etc particles of all substances . What is the basic unit of our universe? This is a problem that has plagued mankind for thousands of years. Formerly people brought up the atomism, but later it has been discovered that the atom can be split, and now it has been demolished to the quark, and the theory of chord can be made, but for the understanding of the basic unit of the universe become more uncertain, and even denied its existence.
However, the basic unit of the universe is necessary! If there is no basic unit, with "no" can be combined into all exist? While it is unclear what it is, since it is real, we first name it as X.
Paradox 1: If the universe is composed of numerous X, then is there gap between any two X? If there is no gap, all X will lose the movement space, but also may produce fusion, the whole universe has become a static big X, if there is a gap, which space is composed of what material?
If we call this gap material is “Y”, then is there gap between any two Y? If there is no gap, Y becomes ether, if there is a gap, then the gap between Y will be named Z … …, which fell into an infinite loop, because the ether proved to be non-existent, then we have to find some Something to fill the gap between X, but this gap cycle is no end.
Paradox 2: the basic unit of the universe X must be able to exercise, otherwise there will be no movement in the universe. Where is the power of X from ? There is a saying that the high-dimensional film caused by the X-movement, where is the power of the membrane from? What is the reason that what energy leads to the movement of the membrane? What is the principle if the reason and energy are intrinsic of the membrane? If it is outside the membrane, whether it is necessary to introduce the movement outside the membrane? What is the principle that reason and energy for the movement of the membrane, … this is another infinite cycle!
Paradox 3: Is the movement of the basic unit X of the universe orderly or disorderly? If it is disorderly, why the composition of the macro by the X, the movement is orderly? Put ten thousand crazy together, can form a neat pace of parade team? If the movement of X is orderly, what is the order of this order? What is the cause of the order? The reason is external or internal? What is the reason for the inner reason? If the external reason … … this is an infinite cycle!
To solve the idea of the paradox: the key to cracking is that we must realize that X composed by at least two different things from the nature! One thing is A and the other is B. Because the nature of A and B is different, so many of the basic unit of the universe will not be integrated into a large X.
A and B have excellent plasticity, can be arbitrarily change their shape according to external circumstances, so there is no gap existed.
There must be a power function between A and B, according to the phenomenon analysis of nature, A and B have the phenomenon of "homogeneous repulsion, heterogeneous absorption “, it is the function of gravity and repulsion, so that X has a movement.
X is bound to do the orderly movement, although in the quantum state, this order is not obvious, but due to a large number of quantum polymerization become into large objects, then numerous small order to complete the quantitative change to qualitative change, so it is performance for orderly state on the macro.
Verification of the idea: "level double watches" test — take two very sophisticated watches, after calibration, one put in the cave, one put on the out of cave, keep the position of two watches at level. After a period of time (depending on the precision of the clock), you will find that the watch go fast in the cave, and the another watch go slow out of the cave
Attached: Horizontal double watches test
Relativism derives two phenomena about time: moving clock running slow and low clock running slow. Its verification is as follows:
![[IMG]](data:image/gif;base64,R0lGODdhAQABAPAAAMPDwwAAACwAAAAAAQABAAACAkQBADs=)
Moving clocks running slow: In 1971, physicists placed the high accurate atomic clock on the plane around the world, and then compared with the clock that put same accurate atomic clock as plane on the ground. The results verified: the time on the plane was slower than in the lab. According to Einstein's theory of relativity, when the speed of the movement is faster, then the time go speed is slower.
Low clock running slow: the physicists of the Unite State America National Institute of Standards and Technology used to a pair of most accurate atomic clocks of the world. In one experiment, the researcher placed two atomic clocks on two table, and then the researcher raised the table face by 33cm than another table, and found The atomic clock runs more slow in the low position than high position, and slow about 90 billion of a second in 79 years. This result demonstrates that Einstein's closer to the source of gravity, the time is going more slow.
In this case, two precise atomic clocks (such as clock used low clock running slow in test ), according to the theory of relativity in the same speed and same height, , two watches will not produce difference in fast and slow. But is that so? You can design a horizontal double watches test to study this problem. As below picture:
Choose a hillside, first burst into a platform of more than10 square meter, and then at the bottom of the platform along the horizontal direction drill a mouth more than 10 meters deep across well in the mountain, a person go in the well, and detect whether have the radiation in the well.
prepare two precision watches, named A and B. Take one of them, placed in the well and another placed outside of the well to the weighing (in order to exclude "space-time distortion”, and there may be exist differences), if no abnormalities, record the temperature inside the well.
take a 10-meter-long steel pipe, one end of the steel pipe placed A watch, the other end placed B watch,after proofreaded time, put the steel pipe into the wells about eight or nine meters and in a level position with leveling. Finally, use the multi-layer heavy metal plate to closed well mouth. The watch that stay outside the hole covered by the seal box, so that the temperature, humidity, magnetic field etc keep the same as inside hole, the experimental steps to complete. After a period of time, compared to AB two watches go time, measure the experimental results.
Forecast: the watch outside the hole go slower than the watch in the hole.
Two watches at the same state of motion and the same horizontal position, according to the theory of relativity, the two watches should be the same time. What reason cause the difference? <<The Theory of Nature’s Mystery>> elucidated the "complex particle" theory can be explained, see the original. This test is very simple, but the significance is extremely important. If successful, mankind will explore the true face of the ultimate unit of the universe, thus recognizing the fundamental structure of the universe and the mode of movement.
Need the original text of <<The Theory of Nature’s Mystery>>, please send email to 1577386889@qq.com
Attn: Jiu Tian Ling Yu
More information, please click the link: http://blog.sina.com.cn/s/blog_72a90e010102wrst.html
Please keep us posted, I will enjoy following your work.
Any approach I use must use the spacetime diagram
because I think it is difficult to represent the relativity-of-simultaneity using boxcars as "moving frames of reference".
Any approach I use must use radar methods
to motivate measurements and the assignment of coordinates.
I think radar methods are more straightforward than lattices of "clocks" and "rods".
(For inertial motions in special relativity, they are equivalent.
However, for more general motions in special and general relativity, they may differ….
and would require more advanced discussion to address.)
In my opinion, the Bondi k-calculus method (with its emphasis on radar measurements) is the best starting point, especially for algebra-based physics. With the k-calculus methods, the standard textbook formulas are straightforward to derive and fall out naturally.
A related but even less well known approach by Geroch (in his General Relativity from A to B) is also a good starting point. Geroch uses radar methods to emphasize the square-interval and give operational interpretations of the geometry of spacetime (e.g., what simultaneity means to an observer) in both Special Relativity and Galilean Relativity. My AJP article (which inspired the Insight https://www.physicsforums.com/insights/relativity-rotated-graph-paper/ ) was my attempt to combine Bondi's and Geroch's approaches.
From here, I would go on to develop the geometry of Minkowski spacetime, while comparing and contrasting with Euclidean geometry, using the [unappreciated] geometry of Galilean spacetime (e.g., https://www.desmos.com/calculator/ti58l2sair … play with the E-slider) …something I call "Spacetime Trigonometry", a large ongoing project with many aspects which generates lots of posters for me at AAPT meetings. (I should really write this up soon… but it would have to be broken into a series of AJP articles.) These are examples of Cayley-Klein geometries, which includes the deSitter spacetimes.. This "unification" can help formalize the numerous analogies mentioned in the literature. In addition, I can develop vector and tensorial methods (algebraically, graphically, and geometrically) in order to make contact with traditional intermediate and advanced presentations of relativity.
To the author, you have exposed different approaches to this body of knowledge. What approach or ways would you use and sequence say for undergraduate instruction.
Great insight.