Resistance in complex geometries

[MrHappyTree]

TL;DR

The influence of the geometry on the electrical resistance of a component.

For the electrical resistance $R$ of an ideal wire, we all know the formula $R=\rho * \frac{l}{A}$. However this is only valid for a cylinder with constant cross sectional area $A$.
In a cone the cross section area is reduced over its height (or length $l$). What is a good general approach for the calculation of resistance of such defined but more complex geometries?

Example:
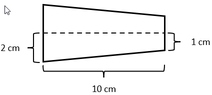
A straight cone has a base radius of 0.02 m and a cut tip with radius of 0.01 m in a height of 0.1 m (sketch). Copper has a resistivity $\rho$ of 17 nΩ⋅m.
First approach: The resistance over the length of the cone sections is between the calculations for a constant radius with 0.01 and 0.02 therefore 5.4 mΩ > R > 1.4 mΩ. Is it possible to add the resistance of infinitely small wire sections together to approximate the shape?

Thank you for your ideas

 

[berkeman]

Welcome to PF.

Summary:: The influence of the geometry on the electrical resistance of a component.

What is a good general approach for the calculation of resistance of such defined but more complex geometries?

Are you familiar with how to do integrations (integral calculus)?

 

[MrHappyTree]

Welcome to PF. Are you familiar with how to do integrations (integral calculus)?

Yes but a bit unsure. So I could integrate the function of the cross section over the length, right?

 

[berkeman]

Yes, integrate all of the resistive elements, but in more complex geometries be mindful of the parallel and series paths.

In the case of a cone, all of the resistive disks will be in series. Can you show your integration so we can check it? Please use LaTeX to post the math here (see the "LaTeX Guide" link at the lower left of the Edit window). Thanks.

 

[MrHappyTree]

Yes, integrate all of the resistive elements, but in more complex geometries be mindful of the parallel and series paths.

In the case of a cone, all of the resistive disks will be in series. Can you show your integration so we can check it? Please use LaTeX to post the math here (see the "LaTeX Guide" link at the lower left of the Edit window). Thanks.

The area is equal to $\pi * r^2$ and the radius $r$ is a function of the length $r(l)$.
To approximate the change in radius, it is taken over a smaller section $dl$ instead of $l$ and sumed up as an integral:
$$R= \int_{0}^{L} \rho\frac{1}{A} \,dl = \rho \int_{0}^{L} \frac{1}{\pi*(r(l))^2} \,dl
= 17 n\Omega m \int_{0}^{0.1} \frac{1}{\pi*(\frac{-0.01}{0.1}*l+0.02)^2} \,dl = 2.70563 m\Omega$$

I guess I got confused about integrating $l/A$, but now it makes more sense :)

 

[berkeman]

Nice. And as a sanity check, you could calculate the resistance of a cylinder that has about the average radius of the conical section to see how close they are...

Note -- since the resistance of each disc varies at $\frac{1}{r^2}$ the average radius number won't equal your integral result, but you can make a correction for that in the approximation...

 

[MrHappyTree]

Exactly! Turned out to be quite simple but knowing how to implement the geometry function helps me a lot. Thanks for checking ^^