Restoring force on a ball connected to two rubber bands

[EnricoHendro]

Homework Statement

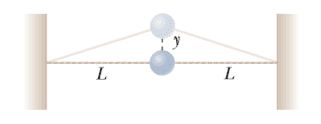
A ball of mass m is connected to two rubber bands, each of length L, each under tension T. The ball is displaced by a small distance y perpendicular to the length of the rubber bands. Assuming the tension does not change, show that the restoring force is -(2T/L)y

Relevant Equations

F=-(2T/L)y

Hello there, I am wondering, in this solution, I guessed that the restoring force is given by that equation in the problem because the vertical component of the force acting on the ball is -2Tsin(x). since sin(x) = y/L with L being the hypotenuse part of the triangle formed by displacing the ball vertically upward. as shown in the figure. I get that intuitively, the restoring force involves only the tension of the rubber band, but why don't we also consider the force of gravity? isn't gravity also somehow act on the system? Or we just ignore it because the gravity is countered by the upward tension of the rubber band?

 

[haruspex]

why don't we also consider the force of gravity?

The question as stated does not indicate whether the diagram is a plan view or an elevation.
Even if it is an elevation, we can modify it slightly by taking the strings as angling down to the mass at equilibrium, then just considering perturbations from that position. If the angle at equilibrium is α then I think the net restoring force becomes $2T\frac yL\cos(\alpha)$, i.e. what matters is the horizontal component of the tension.

 

[EnricoHendro]

The question as stated does not indicate whether the diagram is a plan view or an elevation.
Even if it is an elevation, we can modify it slightly by taking the strings as angling down to the mass at equilibrium, then just considering perturbations from that position. If the angle at equilibrium is α then I think the net restoring force becomes $2T\frac yL\cos(\alpha)$, i.e. what matters is the horizontal component of the tension.

I see. I still don't quite understand the part "by taking the strings as angling down to the mass at equilibrium, then just considering perturbations from that position".

 

[PeroK]

I see. I still don't quite understand the part "by taking the strings as angling down to the mass at equilibrium, then just considering perturbations from that position".

In that case the oscillation would take place about the equilibrium point where the mass naturally hangs.

I'd assume from the diagram that we have a horizontal oscillation in this case.

 

[EnricoHendro]

In that case the oscillation would take place about the equilibrium point where the mass naturally hangs.

I'd assume from the diagram that we have a horizontal oscillation in this case.

oh, I see, so basically, (ignoring our assumption that this particular problem has a horizontal oscillation) because the oscillation would take place about the equilibrium point where the mass naturally hangs (in which the gravitational force is canceled by the balancing force that makes the system in equilibrium), then we can ignore the gravity. Am I getting this right? Because I noticed that the other similar problems which the acceleration is given by force of gravity plus or minus some proportionality constant times distance, the force of gravity always gets ignored when we are trying to find the restoring force or just the angular frequency. (Just like this problem and two other similar problems but involving torques)

 

[haruspex]

I see. I still don't quite understand the part "by taking the strings as angling down to the mass at equilibrium, then just considering perturbations from that position".

Suppose that at equilibrium the strings angle down at angle $\alpha$. $2T\sin(\alpha)=mg$.
If we pull the mass down so as to increase the angle by $\theta$, T not changing much, the net upward force is $F=2T\sin(\alpha+\theta)-mg= 2T(\sin(\alpha)\cos(\theta)+\cos(\alpha)\sin(\theta)-\sin(\alpha))$.
We can approximate $\sin(\theta)$ as $\theta$ and $\cos(\theta)$ as 1:
$F=2T(\sin(\alpha)+\cos(\alpha)\theta-\sin(\alpha))=2T\cos(\alpha)\theta$.

 

[EnricoHendro]

Suppose that at equilibrium the strings angle down at angle $\alpha$. $2T\sin(\alpha)=mg$.
If we pull the mass down so as to increase the angle by $\theta$, T not changing much, the net upward force is $F=2T\sin(\alpha+\theta)-mg= 2T(\sin(\alpha)\cos(\theta)+\cos(\alpha)\sin(\theta)-\sin(\alpha))$.
We can approximate $\sin(\theta))$ as $\theta$ and $\cos(\theta))$ as 1:
$F=2T(\sin(\alpha)+\cos(\alpha)\theta-\sin(\alpha))=2T\cos(\alpha)\theta$.

Oh i see, so we take the trigonometric form of mg which in this case is 2Tsin(x) and then solve it for F. Am I getting this right?

 

[haruspex]

Oh i see, so we take the trigonometric form of mg which in this case is 2Tsin(x) and then solve it for F. Am I getting this right?

Not entirely sure what you mean. Where x is what?
Did you understand all the steps in post #6?

 

[EnricoHendro]

Not entirely sure what you mean. Where x is what?
Did you understand all the steps in post #6?

by x I mean the $\alpha$ .

 

[haruspex]

by x I mean the $\alpha$ .

Ok, and what is "it" that we are solving for F?

 

[EnricoHendro]

Ok, and what is "it" that we are solving for F?

I meant, solve for F using mg = 2Tsin$\alpha$ so we'd get equation $F=2T\sin(\alpha+\theta)-2Tsin$\alpha##

I got my wording all over the place, I apologise. I meant to say solve for F.

 

[haruspex]

I meant, solve for F using mg = 2Tsin$\alpha$ so we'd get equation $F=2T\sin(\alpha+\theta)-2Tsin$\alpha##

I got my wording all over the place, I apologise. I meant to say solve for F.

Then, yes.