Rocker Output-Two Positions with Angular Displacement

[mech-eng]

This is a example from Robert L. Norton's books on machinery: "Design a fourbar Grashof crank-rocker to give 45° of rocker rotation with equal time forward and back, from a constant speed motor input.

Solution
1)Draw the output link O₄B in both extreme positions, B₁ and B₂ in any convenient location, such that desired angle of motion O₄ is subtended

2)Draw the chord B₁B₂ and extend it in either direction.

3)Select a convenient point O₂ on line B₁B₂ extended.

4)Bisect line segment B₁B₂, and draw a circle of that radius about O₂

5)Label two intersection of the circle and B₁B₂ extended, A₁
and A₂

6)Measure the length of the coupler as A₁ to B₁ or A₂ to B₂

7)Measure ground length 1, crank length 2, and rocker length 4.

8)Find the Grashof condition. If non-Grashof, redo steps 3 to 8 with O₂ farther from O₄

9)make a model of the linkage and check its function and transmission angles.

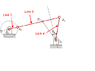
Here is what the mechanism seems

I understand the steps but I can't understand by what step does the mechanism have equal time forward back and forth and how can we understand this mechanism has equal time forward and back. Is there any criteria or formula which show mechanims' back and forth time.

 

[Greg Bernhardt]

I'm sorry you are not generating any responses at the moment. Is there any additional information you can share with us? Any new findings?

 

[Bobbywhy]

I am fairly certain that example 5-1 in the below website explains how to design and to understand the equal times (Grashof condition). Hope this helps:

http://facultad.bayamon.inter.edu/elay/mecn4110/Analytical%20Linkage%20Synthesis.pdf

Cheers, Bobbywhy