Kokobird321
- 3
- 0
Summary:: Classical problem about a pendulum!
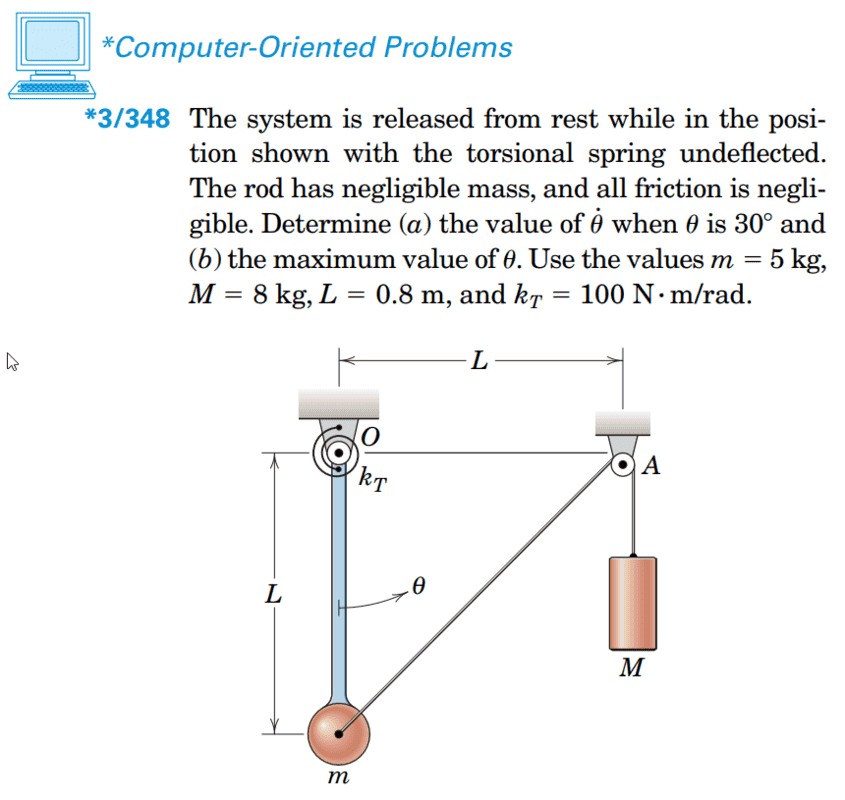
The problem itself:
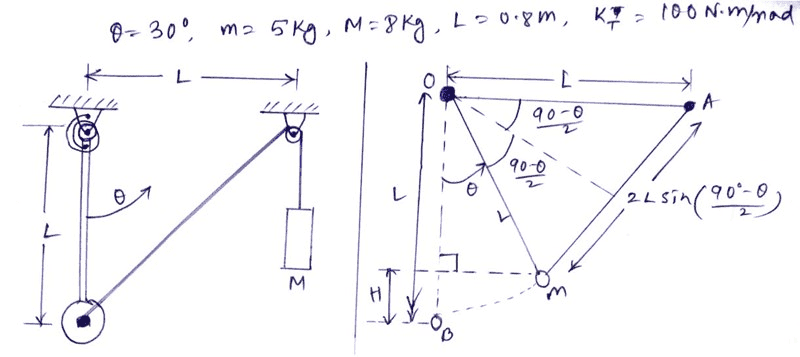
My FBD:
I want to solve the problem with vectors, I think that you can use energy principle somehow. If we define the vector ##\vec{O}_B=\begin{bmatrix}0\\ -1\end{bmatrix}## and define a rotational matrix where
$$R=\begin{bmatrix}cos\varphi & -\sin\varphi\\ \sin\varphi & \cos\varphi\end{bmatrix}$$
just to rotate the vector ##O_B## 30 degrees counterclockwise, but I will need to know its velocity ##\dot{\theta}## when ##\theta=30^{\circ}## somehow. Not sure how to proceed though.
The problem itself:
My FBD:
I want to solve the problem with vectors, I think that you can use energy principle somehow. If we define the vector ##\vec{O}_B=\begin{bmatrix}0\\ -1\end{bmatrix}## and define a rotational matrix where
$$R=\begin{bmatrix}cos\varphi & -\sin\varphi\\ \sin\varphi & \cos\varphi\end{bmatrix}$$
just to rotate the vector ##O_B## 30 degrees counterclockwise, but I will need to know its velocity ##\dot{\theta}## when ##\theta=30^{\circ}## somehow. Not sure how to proceed though.
Last edited: