Soren4
- 127
- 2
I'm confused about this rolling without (or better with) slipping situation. Suppose to have a disk with initial velocity ##v## and angular velocity ##\omega##. The motion is to the right but the angular velocity is counterclockwise.
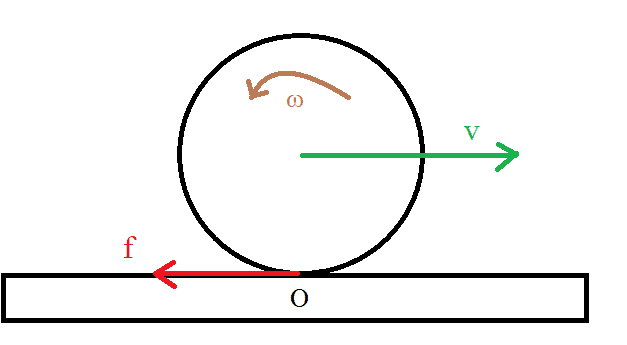
There are no forces acting on the disk besides the kinetic friction##\mathbf{f}##.
Things are ok if I take as pivot point the center of mass.
$$\{\begin{matrix} - \mathbf{f} = m\mathbf{a_{CM}}\\ - \mathbf{r} \times \mathbf{f} =I_{cm} \mathbf{\alpha} \end{matrix}\tag{1}$$
But if I take the point ##O## on the ground, then the kinetic friction has zero torque.
$$\{\begin{matrix} - \mathbf{f} = m\mathbf{a_{CM}}\\ 0 =I_{O} \mathbf{\alpha} \end{matrix}\tag{2}$$
I assumed that the angular velocity (and so $\alpha$) is the same it I take as pivot the center of mass or the point##O##.
If this is the case than parallel axis theorem can be used and $$I_O=I_{cm}+m \mathbf{r}^2$$But there is a contradiction since I get ##\alpha=0## from ##(2)## and ##\alpha\neq0## from##(1)##.
How can that be? Maybe##\alpha## is not the same in the two cases?
There are no forces acting on the disk besides the kinetic friction##\mathbf{f}##.
Things are ok if I take as pivot point the center of mass.
$$\{\begin{matrix} - \mathbf{f} = m\mathbf{a_{CM}}\\ - \mathbf{r} \times \mathbf{f} =I_{cm} \mathbf{\alpha} \end{matrix}\tag{1}$$
But if I take the point ##O## on the ground, then the kinetic friction has zero torque.
$$\{\begin{matrix} - \mathbf{f} = m\mathbf{a_{CM}}\\ 0 =I_{O} \mathbf{\alpha} \end{matrix}\tag{2}$$
I assumed that the angular velocity (and so $\alpha$) is the same it I take as pivot the center of mass or the point##O##.
If this is the case than parallel axis theorem can be used and $$I_O=I_{cm}+m \mathbf{r}^2$$But there is a contradiction since I get ##\alpha=0## from ##(2)## and ##\alpha\neq0## from##(1)##.
How can that be? Maybe##\alpha## is not the same in the two cases?
Last edited: