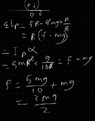SUMMARY
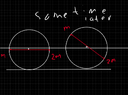
The discussion focuses on the mechanics of a ring with two attached masses (m and 2m) rolling on a rough surface. Participants analyze the center of mass (com) of the ring, which is calculated to be at R/5, and explore the implications for angular acceleration, frictional force, and normal reaction. Key equations such as torque (τ = Iα) and the parallel axis theorem are emphasized for solving the problem. The conversation highlights the importance of drawing free body diagrams (FBD) to visualize forces acting on the system.
PREREQUISITES
- Understanding of rotational dynamics and torque (τ = Iα)
- Familiarity with the parallel axis theorem for moment of inertia calculations
- Ability to calculate center of mass for composite systems
- Knowledge of free body diagram (FBD) construction for analyzing forces
NEXT STEPS
- Study the application of the parallel axis theorem in complex systems
- Learn how to derive angular acceleration in rolling motion scenarios
- Investigate the role of friction in rolling objects on rough surfaces
- Practice drawing and analyzing free body diagrams for various mechanical systems
USEFUL FOR
Students and educators in physics, particularly those focusing on mechanics, as well as engineers and anyone involved in analyzing dynamic systems involving rotational motion.