amjad-sh
- 240
- 13
We know that the rotational inertia I of a certain object is I =∫r∧2 dm where r is the distance between the axis of rotation and the increment of this object that carries a mass dm.
What confuses here is the following:
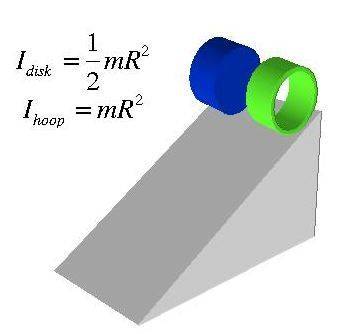
Take for example a hoop of mass M and radius R.
Integration theory gives that I(hoop)=MR∧2.(where the axis is perpendicular to its center)
Now take a disk of radius R and mass M.
Intuition tells that the rotational inertia of the disk will be larger for the disk as integration will perform more summation here.
But the magical result is that I(disk)=0.5MR∧2 which is even less than I(hoop).
So how that comes?
What confuses here is the following:
Take for example a hoop of mass M and radius R.
Integration theory gives that I(hoop)=MR∧2.(where the axis is perpendicular to its center)
Now take a disk of radius R and mass M.
Intuition tells that the rotational inertia of the disk will be larger for the disk as integration will perform more summation here.
But the magical result is that I(disk)=0.5MR∧2 which is even less than I(hoop).
So how that comes?