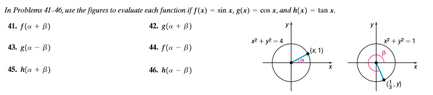karush
Gold Member
MHB
- 3,240
- 5
View attachment 7029
trying to do #41
\begin{align*}\displaystyle
\sin(\alpha + \beta)
&=\sin\alpha \cos \beta
+\cos \alpha \sin \beta\\
&=
\frac{1}{4}\cdot\frac{3}{1}
+\frac{\sqrt{15}}{4}\cdot \frac{\sqrt{10}}{3}
\end{align*}
ok the book answer to this was
$$f(\alpha + \beta)=\frac{1-2\sqrt{6}}{6}$$
but I couldn't derive this
trying to do #41
\begin{align*}\displaystyle
\sin(\alpha + \beta)
&=\sin\alpha \cos \beta
+\cos \alpha \sin \beta\\
&=
\frac{1}{4}\cdot\frac{3}{1}
+\frac{\sqrt{15}}{4}\cdot \frac{\sqrt{10}}{3}
\end{align*}
ok the book answer to this was
$$f(\alpha + \beta)=\frac{1-2\sqrt{6}}{6}$$
but I couldn't derive this