Saltatory Conduction: single AP or not?

[granpa]

this is just an idea that I am presenting. it isn't established fact. the facts are here:
http://www.pubmedcentral.nih.gov/pagerender.fcgi?artid=1392492&pageindex=8

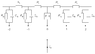
nodes 1234. nodes 3 and 4 and all further nodes are locked. meaning that they will not pass signals.
ap=action potential

t0 node 1 fires producing ap1 which moves at the speed of sound in water. 1500 m/s
t1 ap1 almost instantly reaches node 2 and passes through WITHOUT DELAY
t2 ap1 almost instantly reaches and ends at node 3 and unlocks node 3 (which takes some time)
t3 after 0.1 ms node 2 fires producing ap2 which moves at the speed of sound in water. 1500 m/s
t4 ap2 almost instantly reaches node 3 and passes through WITHOUT DELAY
t5 ap2 almost instantly reaches and ends at node 4 and unlocks node 4 (which takes some time)
t6 after 0.1 ms node3 fires producing ap3 which moves at the speed of sound in water. 1500 m/s

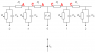
t0 node 1 fires producing ap1
t1 ap1 almost instantly reaches node 2
t1-t3 delay of 0.1 ms at node 2 before it fires
t3 node 2 fires producing ap2
t4 ap2 almost instantly reaches node 3
t4-t6 delay of 0.1 ms at node 3 before it fires

there is therefore only one delay and it is the 0.1 ms one that everyone already agrees on. so it takes 0.1 ms for an action potential at one node to create an action potential at the next node which is typically 1 or 2 mm away. that gives a net speed of 10-20 m/s. if there were no delay at each node then the signal would move at 1500 m/s. the speed of sound in water. (thats just a guess but its certainly at least a good fraction of that speed)

just before each node fires its ap it relocks itself so the ap can only go in one direction and the previous internode can immediately begin to return to its resting state. this is seen in curve C:
http://www.pubmedcentral.nih.gov/pagerender.fcgi?artid=1392492&pageindex=8

 

[somasimple]

https://www.physicsforums.com/showpost.php?p=1897614&postcount=66

This spread takes place with a finite velocity (not necessarily constant) so that graph B becomes later, and graph C earlier towards the distal end of each internode.

finite => delay
+ delay to initiate the next AP since there is a decay in internode.

So I reject, one more time, your point of view. Sorry.

 

[granpa]

i thought we agreed that the speed of the ap through the internode was around 1000 m/s and all the delay came at the node as is suggested by the data here:
http://www.pubmedcentral.nih.gov/pagerender.fcgi?artid=1392492&pageindex=8

 

[somasimple]

i thought we agreed that the speed of the ap through the internode was around 1000 m/s and all the delay came at the node.

It gives 1~2µs for the internode and since the decay is quite 1/3 => total delay around 20 µs.

 

[granpa]

according to this:
http://www.pubmedcentral.nih.gov/pagerender.fcgi?artid=1392492&pageindex=8
the delay at the node is about 0.1 ms or 100 microseconds. a 20 microsecond delay would be almost negligible

 

[granpa]

travelling at 1000 m/s an ap will travel the 1-2 mm from node to node in about 1 or 2 microseconds. so i guess we agree on that. whether decay results in a delay i don't know but i don't see what it matters. the inherent delay at the node swamps it out anyway.

i fail to see what any of this has to do with the idea that nodes lock and unlock

 

[somasimple]

whether decay results in a delay i don't know but i don't see what it matters.

A lot, since the threshold will be reached later at next node.

 

[atyy]

HH model for unmyelinated axon:
-Describes AP at a point and its propagation.
-Considers active and passive circuit components uniformly distributed along the axon.
-Is a wave equation with a well-defined propagation velocity which matches experiement.
-Reduces in a certain limit to the linear passive cable equation which does not have a well defined velocity.

HS model for myelinated axon
-Nodes active, internodes passive
-Internodes considered as resistor and capacitor in parallel (I think I know what they mean, but agree with somasimple it's not obvious), and apparently equivalently with an equation that resembles the linear passive cable equation.
-Expected backwards propagation from node into internode is apparently seen in the data and discussed.
-No explicit calculation of internode velocity, but heuristic and dimensional arguments are given for its form.

FH model data for myelinated axon
-FH model is standard reference for myelinated axon
-Only FH 1964 seems to be available to me, and does not describe propagation, but there may be other FH papers.

 

[granpa]

not much later. not enough to make any difference. the delay at the node is already 100 microseconds anyway. i don't see what internode delay has to do with anything at all much less whether nodes lock or unlock.

 

[granpa]

-Expected backwards propagation from node into internode is apparently seen in the data and discussed..

http://www.pubmedcentral.nih.gov/pagerender.fcgi?artid=1392492&pageindex=8
but the backward propagation that is seen (at least in the data i saw) isn't a backward propagating ap. its an anti-ap. it doesn't depolorize the axon. it returns it to its resting state.

but that's not the issue at the moment.

 

[atyy]

Why the capacity is omitted since it is 40 time greater than at node?

Capacity is not omitted - they are discussing resistor and capacitor in parallel as a model for the internode.

 

[Dale]

HH model for unmyelinated axon:
-Describes AP at a point and its propagation.
-Considers active and passive circuit components uniformly distributed along the axon.
-Is a wave equation with a well-defined propagation velocity which matches experiement.
-Reduces in a certain limit to the linear passive cable equation which does not have a well defined velocity.

Hi atyy, do you by any chance have a link for this? None of the variants of the HH models that I have seen have any spatial terms, but it has been years since I studied this stuff. I would be very interested to see a single model that includes the voltage-gated channels and spatial terms.

 

[atyy]

Hi atyy, do you by any chance have a link for this? None of the variants of the HH models that I have seen have any spatial terms, but it has been years since I studied this stuff. I would be very interested to see a single model that includes the voltage-gated channels and spatial terms.

The HH paper discussing AP propagation in an unmyelinated axon doesn't seem to be free online, unlike the others. I learned about this from somasimple, haven't read it, but looks sensible on a quick scan: http://butler.cc.tut.fi/~malmivuo/bem/bembook/ .

I'll summarise the argument presented by Koch (Biophysics of Computation, OUP 1999) [V_xx is second partial of V wrt x, I haven't bothered about correct signs]:

1. i_m~V_xx

2. i_m~V_t+F(V), where F(V) represents the HH model for the AP at a point, including terms that look like dp/dt~f(p)

3. So V_t~V_xx+F(V)

"no general analytical solution is known ... Hodgkin and Huxley only had access to a very primitive hand calculator ... Instead they considered a particular solution to these equations ... postulated the existence of a wave solution ... V_xx~V_tt ... [more steps until an ordinary DE is also obtained] ... Hodgkin and Huxley iteratively solved this equation until they found a value of u leading to a stable propagating wave solution. In a truly remarkable test of the power of their model, they estimated 18.8 m/s at (18.3^oC) ... a value within 10% of the experimental value of 21.2 m/s ..."

" ... more than 10 years later that Cooley, Dodge and Cohen solved the full partial differential equation numerically ..."

It boggles my mind they did that with a "primitive hand calculator"?!

 

[atyy]

I think I may finally understand somasimple's "discontinuity" objection - it makes sense to me if "discontinuous" means "non-analytic".

Linear passive cable equation: V_xx~V_t, which is a linear parabolic partial differential equation.

HH equation: V_xx~V_t+F(V,p,dp/dt), where p are the HH point conductance parameters. The considerations in its derivation are the same as in deriving the cable equation, but it is not parabolic. This is usually called the HH equation only if p is not a function of x, but I will refer to it as the HH equation even for p(x).

For an unmyelinated axon, some parameter like the density of sodium channels p_n is spatially constant.

For a myelinated axon, the spatial distribution of sodium channels can presumably be modeled by p_n(x), which if analytic will approach zero only asymptotically, and the equation will not be exactly parabolic for any axon segment, and we cannot do an exact separation into "active" and "passive" compartments (HS discuss this, but in different language, they say the internode may be active, but not active enough for current to lead voltage).

If p_n(x) is smooth but not analytic, then it can be exactly zero over some internode segment, and the equation will reduce exactly to the cable equation. In this case we can do an exact separation into "active" and "passive" compartments.

Presumably since the full analytical solution is not known, whether one chooses the parameter to be smooth and analytic, or smooth but not analytic, will be a matter of numerical convenience, since the difference will probably not be experimentally detectable.

 

[Dale]

3. So V_t~V_xx+F(V)

OK, that makes sense. The V_t~V_xx part is the cable equation and the F(V) part is what I knew as the HH model. I just hadn't seen them put together like that, but it is pretty obvious when someone else points it out for you

 

[granpa]

just thought this was interesting:

http://www.ncbi.nlm.nih.gov/pubmed/314337

Using a special albumin technique, nodes of Ranvier have been examined within frog skeletal muscle, sciatic nerve and rat and frog cerebrum. Initial segments have been examined in cerebrum of frog and rat. Mictotubules usually run longitudinally through these regions, but within the bare area of the intramuscular node of Ranvier, annular or helical bundles of microtubules run in a marginal band at right angles to the more centrally placed longitudinal microtubules. These nodal bare areas show a pronounced convexity and it is suggested that the annular microtubules serve to maintain this convexity during muscle contraction.

http://www.ncbi.nlm.nih.gov/pubmed/...nkpos=2&log$=relatedarticles&logdbfrom=pubmedThe relationship between the degree of nodal narrowing and the changes in the structure of the axonal cytoskeleton was studied in 53 fibres of mouse sciatic nerve. Nodal narrowing increased with increasing fibre calibre to reach about 20% of the internodal area in the thicker fibres. The narrowing corresponded quantitatively to a decreased number of nodal neurofilaments. Nodal microtubule numbers varied greatly, and a majority of fibres had considerably (approximately 55%) more microtubules in their nodal profile than in the internode

 

[somasimple]

Capacity is not omitted - they are discussing resistor and capacitor in parallel as a model for the internode.

http://butler.cc.tut.fi/~malmivuo/bem/bembook/21/21.htm
Sorry, but I do not see it.

Granpa,
It is.

 

[granpa]

you do realize that the attached image in your last post, the one from the website here:
http://butler.cc.tut.fi/~malmivuo/bem/bembook/21/21.htm

(in the case of dc, and neglecting the fh at the node, and using the water analogy for current) is just a description of a long empty and leaky pipe. you turn on the water and it takes a while before any comes out the other end.

it says the internode is just modeled as a resistor. the capacitors are for the nodes. doesn't make much sense to me.

 

[somasimple]

I think I may finally understand somasimple's "discontinuity" objection - it makes sense to me if "discontinuous" means "non-analytic".

Not at all.
http://www.sosmath.com/calculus/limcon/limcon05/limcon05.html" is a prerequisite for an electrical signal in a wire/cable.
There is discontinuities at internode/node junctions when the signal leaves the internode entering in the node and when it leaves the node entering to the next internode.

 

[somasimple]

it says the internode is just modeled as a resistor.

That is the problem I'm pointing out.
Normally the nodes are connected to external milieu.

 

[atyy]

http://butler.cc.tut.fi/~malmivuo/bem/bembook/21/21.htm
Sorry, but I do not see it.

The above doesn't even model most nodes as active. HS discuss resistance and capacitance of the internode, and it is very important for them to come to the conclusion that the internode is passive, or at least much less active than the nodes (p328 bottom paragraph through p329).

There is discontinuities at internode/node junctions when the signal leaves the internode entering in the node and when it leaves the node entering to the next internode.

In the data or in someone's model?

 

[somasimple]

The above doesn't even model most nodes as active. HS discuss resistance and capacitance of the internode, and it is very important for them to come to the conclusion that the internode is passive, or at least much less active than the nodes (p328 bottom paragraph through p329).

Adding a capacitor doesn't change the passivity but it is missing (I added the table 2)

In the data or in someone's model?

Both.
Edit: In the model a node is connected to 2 internodes and must be at the same potential.
In data: the end of an internode is not at the same potential than the beginning of the next internode.

 

[somasimple]

HS discuss resistance and capacitance of the internode, and it is very important for them to come to the conclusion that the internode is passive, or at least much less active than the nodes (p328 bottom paragraph through p329).

I agree.
Edit:
http://www.pubmedcentral.nih.gov/articlerender.fcgi?artid=1473353
see figure 1 for a more appropriate electric model.

 

[granpa]

" The conduction velocity also is relatively insensitive to the internodal length"

i like that.

 

[somasimple]

Here is the problem:
And, active node or not, it does not change the passive internodes, does it?

 

[somasimple]

" The conduction velocity also is relatively insensitive to the internodal length"

i like that.

Me too. It is normal in a body that moves and thus stretches or shrinks nerves: The message must be delivered (safety factor) and insensitivity to internal motion.

 

[granpa]

if the impulse does indeed move at or just below the speed of sound in water or is even just limited by the speed of sound in water then that would mean that significant amounts of water are being moved. the mass of the water would add an inductance to the equivalent circuit. or so it seems to me.

 

[somasimple]

if the impulse does indeed move at or just below the speed of sound in water or is even just limited by the speed of sound in water then that would mean that significant amounts of water are being moved. the mass of the water would add an inductance to the equivalent circuit. or so it seems to me.

Why an inductance?

 

[granpa]

because inductance is the electrical equivalent of mass.

 

[granpa]

just think of a sound wave as passing through a series of masses connectedby springs. the mass effect becomes obvious.