MHB Samantha's question at Yahoo Answers involving related rates

[MarkFL]

Here is the question:

A security camera is centered 50 ft above a 100 foot hallway... Related Rates Question! HELP?

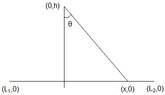
A security camera is centered 50 ft above a 100 foot hallway. It rotates back and forth to scan from one end of the hallway to the other. It is easiest to design the camera with a constant angular rate of rotation, but this results in a variable rate at which the images of the surveillance area are recorded. Therefore, it is desirable to design a system with a variable rate of rotation and a constant rate of movement of the scanning beam along the hallway. What rate of rotation is necessary to accomplish this? Verify you solution with some specific constant rates of movement.

Here is a link to the question:

A security camera is centered 50 ft above a 100 foot hallway... Related Rates Question! HELP? - Yahoo! Answers

I have posted a link there to this topic so the OP can find my response.

 

[MarkFL]

Hello Samantha,

I would solve this problem in more general terms, derive a formula, then plug the given data in.

Suppose we let the camera be $h$ units above the hallway, and the hallway extends $L_1$ units to the left of the camera and $L_2$ units to the right. Let the angle $\theta$ of the camera's angle of rotation be zero radians directly below the camera.

Please refer to the following diagram:

View attachment 4087

Hence the angle of rotation will be confined to the interval:

$\displaystyle -\tan^{-1}\left(\frac{L_1}{h} \right)\le\theta\le\tan^{-1}\left(\frac{L_2}{h} \right)$

We can see that for any positive value of $h$ and any finite values of $L_1$ and $L_2$, we must have:

$\displaystyle -\frac{\pi}{2}<\theta<\frac{\pi}{2}$

Now, letting the position of the camera's beam on the floor of the hallway be $(x,0)$, we have the following relationship between this position and the angle of rotation:

$\displaystyle \tan(\theta)=\frac{x}{h}$

Differentiating with respect to time $t$, we find:

$\displaystyle \sec^2(\theta)\frac{d\theta}{dt}=\frac{1}{h}\frac{dx}{dt}$

We require $\displaystyle \left|\frac{dx}{dt} \right|=k$ where $0<k\in\mathbb{R}$. Hence:

$\displaystyle \frac{d\theta}{dt}=\frac{k}{h}\cos^2(\theta)=\frac{k}{h}\frac{h^2}{x^2+h^2}=\frac{kh}{x^2+h^2}$

Using the given data, we find the angle of rotation will vary from:

$\displaystyle -\frac{\pi}{4}\le\theta\le\frac{\pi}{4}$

where:

$\displaystyle \left|\frac{d\theta}{dt} \right|=\frac{50k}{x^2+50^2}$

and:

$\displaystyle -50\le x\le50$

 

[MSW]

Hello Samantha,

I would solve this problem in more general terms, derive a formula, then plug the given data in.

Suppose we let the camera be $h$ units above the hallway, and the hallway extends $L_1$ units to the left of the camera and $L_2$ units to the right. Let the angle $\theta$ of the camera's angle of rotation be zero radians directly below the camera.

Please refer to the following diagram:
Hence the angle of rotation will be confined to the interval:

$\displaystyle -\tan^{-1}\left(\frac{L_1}{h} \right)\le\theta\le\tan^{-1}\left(\frac{L_2}{h} \right)$

We can see that for any positive value of $h$ and any finite values of $L_1$ and $L_2$, we must have:

$\displaystyle -\frac{\pi}{2}<\theta<\frac{\pi}{2}$

Now, letting the position of the camera's beam on the floor of the hallway be $(x,0)$, we have the following relationship between this position and the angle of rotation:

$\displaystyle \tan(\theta)=\frac{x}{h}$

Differentiating with respect to time $t$, we find:

$\displaystyle \sec^2(\theta)\frac{d\theta}{dt}=\frac{1}{h}\frac{dx}{dt}$

We require $\displaystyle \left|\frac{dx}{dt} \right|=k$ where $0<k\in\mathbb{R}$. Hence:

$\displaystyle \frac{d\theta}{dt}=\frac{k}{h}\cos^2(\theta)=\frac{k}{h}\frac{h^2}{x^2+h^2}=\frac{kh}{x^2+h^2}$

Using the given data, we find the angle of rotation will vary from:

$\displaystyle -\frac{\pi}{4}\le\theta\le\frac{\pi}{4}$

where:

$\displaystyle \left|\frac{d\theta}{dt} \right|=\frac{50k}{x^2+50^2}$

and:

$\displaystyle -50\le x\le50$

Mark,How did you arrive at
$\displaystyle \frac{k}{h}\frac{h^2}{x^2+h^2}$
From $\displaystyle \frac{k}{h}\cos^2(\theta)$

 

[MarkFL]

Mark,

How did you arrive at
$\displaystyle \frac{k}{h}\frac{h^2}{x^2+h^2}$
From $\displaystyle \frac{k}{h}\cos^2(\theta)$

If we have defined:

$$\tan(\theta)=\frac{x}{h}$$

This means in the right triangle the side opposite from $\theta$ is x and the side adjacent is $x$. By Pythagoras, the hypotenuse must then be $$\sqrt{x^2+h^2}.$$

As cosine is defined to be the ratio of adjacent to hypotenuse, we then find:

$$\cos(\theta)=\frac{\text{adjacent}}{\text{hypotenuse}}=\frac{h}{\sqrt{x^2+h^2}}$$

Hence:

$$\cos^2(\theta)=\frac{h^2}{x^2+h^2}$$

Does this make sense?

 

[MSW]

If we have defined:

$$\tan(\theta)=\frac{x}{h}$$

This means in the right triangle the side opposite from $\theta$ is x and the side adjacent is $x$. By Pythagoras, the hypotenuse must then be $$\sqrt{x^2+h^2}.$$

As cosine is defined to be the ratio of adjacent to hypotenuse, we then find:

$$\cos(\theta)=\frac{\text{adjacent}}{\text{hypotenuse}}=\frac{h}{\sqrt{x^2+h^2}}$$

Hence:

$$\cos^2(\theta)=\frac{h^2}{x^2+h^2}$$

Does this make sense?

Perfect sense! Thank you!