- #1
squenshl
- 479
- 4
Homework Statement
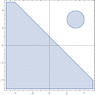
Consider the sets ##A = \left\{(x_1,x_2) \in\mathbb{R}^2: x_1+x_2 \leq 1\right\}## which is a straight line going through ##(0,1)## and ##(1,0)## and ##B = \left\{(x_1,x_2) \in\mathbb{R}^2: (x_1-3)^2+(x_2-3)^2 \leq 1 \right\}## which is a circle of radius ##1## centred at ##(3,3).##
1. Are the sets ##A## and ##B## convex? Are they closed? Are they compact?
2. What is ##A\cap B##?
3. Is it possible to find a hyperplane that separates ##A## and ##B##? That strictly separates them?
4. If they can be strictly separated then give one hyperplane that strictly separates the sets. If they can be separated but cannot be strictly separated then give one hyperplane that separates the sets and explain why they cannot be strictly separated. If they cannot be separated then explain why they cannot be separated.
Homework Equations
The Attempt at a Solution
1. I know they are convex, closed and compact by drawing a diagram. Is that sufficient enough or would I have to show it using maths? If so, how would I do that ? Some guidance would be great!
2. That is just the empty set.
3. Yes it is possible to separate them but not sure about if it strictly separates them.
4. The line ##x_1+x_2=2## is a hyperplane that strictly separates them I think. Is it possible 2 have sets that are both separated and strictly separated by a hyperplane. If not then obviously its just the first part of question 4 "If they can be strictly separated then give one hyperplane that strictly separates the sets".
Thanks a lot for the help!