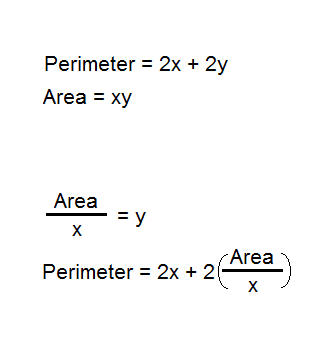LearninDaMath, you seem to be giving credit where you believe it's deserved, but as a matter of fact, I'm only giving you special treatment because this doesn't look like it's a homework problem, but rather a curiosity that you have. In any other case, myself and other homework helpers would be giving you hints to nudge you in the right direction as opposed to explaining it in full detail.
Similarly, your example about getting help to find your destination isn't really a valid representation of what's happening. It is against the forum rules to just give students the answers to their homework problems (and yes, I've broken those per the reasoning above), so what you should be hoping to get at most is for that gas station manager to tell you you're heading in the wrong direction, and then stop right there. You'd have to figure the rest out for yourself, and if you are having further troubles, then you can ask for more help on those specific sub-problems.
Now, if someone has been leading you towards a wrong answer, then I can understand if you want to avoid their posts, but if they were honestly trying, then they at least deserve acknowledge in that regard. I'm not exactly sure what you were referring to when you said that someone was giving you the wrong answers though. I don't see any wrong answers, just confusion, as I had as well with my first post in this thread.
Anyway, now onto your questions:
LearninDaMath said:
Statement 1: For any given area of 16 and greater, there will always be one (and only one) specific set of dimensions (x,y) such that area = perimeter (xy = 2x + 2y).
The short answer is yes, but to understand why this is so, we'll need to introduce the concept of functions.
Firstly, the equation we're dealing with (xy=2x+2y) needs to be a function. If we make a variable x or y the subject (it's customary to make y the subject) then we have,
y=\frac{2x}{x-2}
And this is known to be a function. What that means is that for any x value, there is only 1 y value that will pop out.
But how do we know this? Well, this is called a rational function, but a little bit of algebra can simplify it in a way that'll be easier to grasp.
y=\frac{2x}{x-2}
=\frac{2x-4+4}{x-2}
=\frac{2(x-2)+4}{x-2}
=\frac{2(x-2)}{x-2}+\frac{4}{x-2}
=2+\frac{4}{x-2}
And it's trivial that \frac{4}{x-2} is a function, thus the equation we're dealing with is a function. This means for any x (length) we input, we will get an appropriate y value (again, except for x=2 or y=2).
Secondly, if we want to know that for any given A (with appropriate restrictions on A) there is a unique solution to the Area=Perimeter equation, we need to look back at the quadratic we got after plugging A=xy into the equation. So, from the previous post I made,
2x^2-Ax+2A=0
Now we want to know whether this is a function (given A\geq 16 and x>0. Well, when we make x the subject, we get
x=\frac{A\pm\sqrt{A^2-16A}}{4}
So how do we know whether this is a function or not? That is, for any given A, is there just one value of x that pops out? If it's hard to tell, try breaking it up like this:
x=\frac{A}{4}\pm\frac{\sqrt{A^2-16A}}{4}
So we have x equalling to some number \pm another number, which means x equals 2 numbers! Unless the part after the \pm is equal to 0, but that only happens when A^2-16A=0 which is at A=16. So, for any A there are two values of x! Surely this means that we can get two sets of (x,y) values for each A? Well, no. There's something we're forgetting

So let's say we chose A=18 (we know a solution set for this is (x,y)=(6,3) ), if we plug this into the equation we get
x=\frac{18\pm\sqrt{18^2-16\cdot 18}}{4}
And simplifying,
=\frac{18\pm\sqrt{18(18-16)}}{4}
=\frac{18\pm\sqrt{18\cdot 2}}{4}
=\frac{18\pm\sqrt{36}}{4}
=\frac{18\pm 6}{4}
x=6, 3
Notice that we found both the values 6 and 3 for x. This is because we haven't specified any added restrictions on x such as the length is always bigger than the width or anything similar. We could've fooled ourselves into thinking that there were two solution sets when in fact the two solution sets we were getting would be (6,3) and (3,6), but we consider both these rectangles to be equivalent, so we don't count that as separate solutions.
So in fact, that equation is giving us the solution sets for both length and its corresponding width (you can choose whether length is going to be the + and width - or vice versa).
And so finally, since the restricted domain (let's assume the length x is longer than the width)
x=\frac{A+\sqrt{A^2-16A}}{4}
is a function, then your question is answered.
LearninDaMath said:
Statement 2: Given the shape of a rectangle, if you let x = any positive value, there will always be some corresponding positive y value, such that the dimensions (x,y) satisfy area = perimeter.
Yes, because xy=2x+2y thus y=\frac{2x}{x-2} is a continuous function (within its domain, so we exclude the value x=2). This means that for any x-value you choose, there will be some y-value to go with it. There are no holes in the function.
LearninDaMath said:
Statement 3: The ratio between height and length of a rectangle can be used to rewrite xy = 2x + 2y into an equation in terms of x, (such as x = y so that x(x) = 2x + 2(x)). So that the x dimension of the described rectangle can be found, which can then be used to find the specific y value that let's the equation area = perimeter be true.
I actually touched on the length to width ratios in one of my previous posts. If we want to restrict ourselves to rectangles where the length is three times the width, then we use y=3x and substitute that into the equation, giving us x(3x)=2x+2(3x)
3x^2=2x+6x
With this quadratic, if you solve for x you'll be given the value of the length such that Area=Perimeter when the length is three times the width. It only happens at one value (solve the quadratic and toss out unwanted values, such as x=0).
As I also added before, you can try the same procedure for all possible ratios, which we can denote as m or anything else you prefer. You'll find that when you get to your answer, it will in fact be a function.
In summary, yes. And just to add, when you say ratio x=y that means you're looking for the specific case when the rectangle is a square (x=y means length=width).
LearninDaMath said:
Statement 4: And in the example of ratio x = y, [x(x) = 2x + 2x] ==> [x^2 = 4x] where x = 4 and y = 4. You can not use the fact that the sides are of a specific proportion in order to assume that any value of x will satisfy Area = Perimeter. In other words, just because the sides are x = y, it doesn't mean that 5 = x and 5 = y will satisfy Area = Perimeter. As a second example, just because (6,3) satisfies [y = 2x] and thus [x(2x) = 2x + 2(2x)] = [Area = Perimeter], it doesn't mean that (8,4), (10,5), (12,6) are going to satisfy Area = Perimeter.
Yes, you're right. This is the corollary to all the points we've covered before. We've shown that for any given area, there is only one possible rectangle that can satisfy area=perimeter, and also shown that given any length (except 2) there is only one value of width that'll satisfy area=perimeter, thus, we can't just choose any combination of values and expect it to satisfy area=perimeter.
It always has to satisfy xy=2x+2y
LearninDaMath said:
Statement 5: I can be given a random Area (greater than 16) and by way of algebra, find the two dimensions that satisfy Area = Perimeter.
Yes, that's the same as statement 1.
LearninDaMath said:
Statement 6: I can start with a value representing x, and from there, use algebra to determine the a y value such that area = perimeter, even if I haven't yet determined the specific value of area. And once I have found the y value corresponding to the x value, a simple multiplication will tell me the area (and of course perimeter).
Yes. What you have there are 3 unknowns: length, width, area. Once you know 2 of them, you can solve the last one. So this means that you can have length and area, and correspondingly find width.
LearninDaMath said:
Statement 7: Given [Area = xy] and [Perimeter = 2x + 2y] Area and Perimeter do not have to be equal to each other in order to substitute one into the other. Confirmed by a sample case where if I have a rectangle with area 50 and give it dimensions x = 5 and y = 10, the corresponding perimeter will be 30, and since 50 ≠ 30, then Area ≠ Perimeter. However, I can still arrange Area = 10(5) into Area/10 = 5 and substitute into [Perimeter = 2x + 2y] to get [Perimeter = 2x + 2(Area/10)] or [30 = 2(10) + 2(50/10)] ==> [30 = 30]
Area and perimeter are hardly ever equal to each other. This is obvious from the fact that xy and 2x+2y are considerably different functions from each other (although for some specific values, they do intersect, which gives us (x,y) when area=perimeter).
You can solve for anything you want though. You can find when area is twice the perimeter, so xy=2(2x+2y) or when the perimeter is k times more than area, so kxy=2x+2y. Just because we equate these equations doesn't mean that for any value of x,y they're going to be equal. When we equate them, we're assuming they're equal, so if you chose values that don't satisfy the equality, then you'll get something that doesn't equate, such as 1=0.
Also, you really aren't asking a question here, you're just confirming something that you've already come to understand on your own. So I guess I can say, yes, you're right

Good luck trying to take all that in!
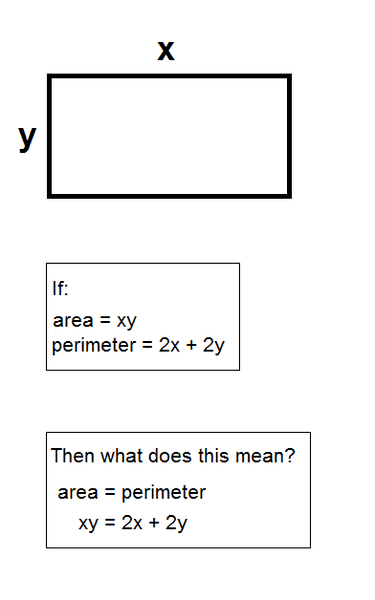 Can this ever be true? That xy = 2x+2y?
Can this ever be true? That xy = 2x+2y?