Momo 6aye3
- 3
- 1
Hi!
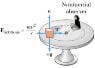
I am currently working on a project that includes rotating a water-filled container. The container is NOT spinning about its vertical axis, but about the vertical axis of the rotating disc.
I am aware that the surface shape of water in a rotating bucket takes the shape of a parabola when it is rotated about its axis, but what is the effect when rotated on a vertical axis that isn't its own?
My intuition tells me that it will be a part of a parabola whose vertex lies on the y-axis of the disc, but I am not sure.
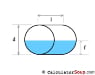
Also, will the shape of the container affect the shape of the surface of the water? (The cylinder is placed horizontally on the disc).
Thank you!
I am currently working on a project that includes rotating a water-filled container. The container is NOT spinning about its vertical axis, but about the vertical axis of the rotating disc.
I am aware that the surface shape of water in a rotating bucket takes the shape of a parabola when it is rotated about its axis, but what is the effect when rotated on a vertical axis that isn't its own?
My intuition tells me that it will be a part of a parabola whose vertex lies on the y-axis of the disc, but I am not sure.
Also, will the shape of the container affect the shape of the surface of the water? (The cylinder is placed horizontally on the disc).
Thank you!