Richie Smash
- 293
- 15
Homework Statement
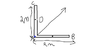
The figure shown consists of two rods at right angles to each other and each is uniform of 2m length.
D and E are the midpoints of AC and AD
Draw the line of action of the weight of the arrangement relative to A, B,C, D and E when it is
(a) Suspended from A and in equilibrium
(b) Suspended from D and in equilibrium
(ii) Clearly indicate the position of the centre of gravity of the arrangement relative to A,B,C,D and E
Homework Equations
The Attempt at a Solution
On my diagram I have drawn one big line from A and I believe that would be the line of action?
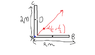
The arrows in red indicate the lines of actions from each point, however they want the line of action of the entire weight of the arrangement, so clearly the centre of gravity will indicate where this weight is
From there I can draw the line of action I believe, I know that the centre of gravity is in the middle of the uniform object but I only have the centre of Gravity for the two individual planks, I'm not sure how to get the CG for the entire thing.
Also I'm not sure how to drawn the two different lines of actions It is rather confusing.
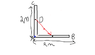
But actually, in my opinion I would say that the centre of gravity of the entire thing is at point A?
I edited the photo actually, and just have drawn the line of action when it is suspended at A and the centre of gravity, indicated in blue