Sign mistake when computing integral with differential forms

[beefbrisket]

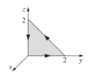
The question provides the vector field $(xy, 2yz, 3zx)$ and asks me to confirm Stokes' theorem (the vector calc version) but I am trying to use the generalized differential forms version. So, I am trying to integrate $\omega = xy\,dx + 2yz\,dy + 3zx\,dz$ along the following triangular boundary $\partial \Sigma$:

First, I try to find $\int_\Sigma d\omega$. I computed $d\omega = x\,dy\,dx + 2y\,dz\,dy + 3z\,dx\,dz$ which simplifies to $2y\,dz\,dy$ on $\Sigma$. However, integrating over the appropriate domain of $y,z$ with that differential gives 8/3 when the answer should be -8/3. I suspect my mistake is in not first reordering $2y\,dz\,dy$ to $-2y\,dy\,dz$ before integrating, but I'm not clear on the rational behind doing so. I am missing some intuition on what $2y\,dz\,dy$ and $-2y\,dy\,dz$ "are." In any case, where have I gone wrong?

 

[jedishrfu]

Could be from differential forms convention ie $dxdy$ , $dydz$ , and $dzdx$ are in the positive direction but $dydx$ , $dzdy$ , and $dxdz$ are in the negative direction.

$dxdy = -dydx$ , $dydz = -dzdy$ and $dzdx = -dxdz$

 

[beefbrisket]

Could be from differential forms convention ie $dxdy$ , $dydz$ , and $dzdx$ are in the positive direction but $dydx$ , $dzdy$ , and $dxdz$ are in the negative direction.

$dxdy = -dydx$ , $dydz = -dzdy$ and $dzdx = -dxdz$

In one of Weintraub's intro texts on differential forms he introduces the "fundamental correspondence" between vectors and differential forms in R^3 (haven't been able to find any other sources using this name) and for the correspondence between vectors and 2-forms he indeed uses that ordering. Is there some intuitive explanation for why it is so? I imagine sometimes we would need to use the negative directions too, any idea how I would know which is the form I am after?

 

[jedishrfu]

There's a vector convention for surfaces as shown in this wikipedia article:

https://en.wikipedia.org/wiki/Curl_(mathematics)

Counterclockwise ie righthand rule where fingers curl and point in the direction of integration and the thumb points in the direction of the normal to the surface considered the positive direction.

You can see it more clearly in the wedge product ie $dx \wedge dy$ which is anticommutative by definition.

Differential forms was a cleaner way of handling vector analysis. (my guess)